PAC自学架构
PAC(Probably Approximately Correct)架构借助于样品维数(欲达至近似于截叶须要的样品点数量)和自学演算法的天数内部空间维数(倚赖基本概念类排序则表示的付出)来表述可自学的基本概念类。
PAC自学数学模型
样品: X\mathcal{X}
条码: Y\mathcal{Y} ,该处只探讨二进行分类的情形,Y={0,1}\mathcal{Y}=\{0,1\}
基本概念: X→Y\mathcal{X}\rightarrow\mathcal{Y} ,指两个从X\mathcal{X}到Y\mathcal{Y}的映射
基本概念类:C,可能想要自学的基本概念的集合
分布:D,假设所有样品独立同分布,该分布固定但未知
假设集:H,固定的、所有可能的基本概念组成的集合H,H与C可能一致,也可能不一致(一致是指假设集中包含了待自学的基本概念,我理解为C∈HC\in H )
泛化误差:
给定两个假设 h∈Hh\in H ,两个目标基本概念 c∈Cc\in C ,以及两个潜在的分布D,则h的泛化误差或风险表述为 R(h)=Prx∼D[h(x)≠c(x)]=Ex∼D[lh[x]≠c[x]]R(h)=\Pr_{x\sim D}[h(x)\not=c(x)]=\mathop{E}_{x\sim D}[l_{h[x]\not=c[x]}] ,因为分布D和目标基本概念c均未知,泛化误差无法直接获得
经验误差:
给定两个假设 h∈Hh\in H ,两个目标基本概念 c∈Cc\in C ,以及两个样品集 S=(x1,…,xm)S=(x_1,\dots,x_m) ,则h的经验误差或经验风险为 R^(h)=1m∑i=1mlh(xi)≠c(xi)\hat{R}(h)=\frac{1}{m}\sum_{i=1}^ml_{h(x_i)\not=c(x_i)}
对于固定的 h∈Hh\in H ,在样品独立同分布的情形下,样品集上经验误差的期望就等于 E[R^(h)]=R(h)E[\hat{R}(h)]= R (h) ,对于样品集S中任意样品x: ES∼Dm[R^(h)]=1m∑i=1mES∼Dm[lh(xi)≠c(xi)]=1m∑i=1mES∼Dm[lh(x)≠c(x)]=Ex∼D[lh(x)≠c(x)]=R(h)\mathop{E}_{S \sim D^m }[ \hat{R}(h) ]= \frac{1}{m} \sum_{i=1}^{m} \mathop{E}_{S \sim D^ m }[l_{h(x_i) \not=c(x_i)}]=\\ \frac{1}{m}\sum_{i=1}^{m} \mathop{E}_{S\sim D^m}[l_{h(x)\not=c(x)}]=\mathop{E}_{x \sim D}[l_{h(x) \not =c(x)}]=R(h)
将对任意元素 x∈Xx\in\mathcal{X}进行则表示的排序维数(如x的维度)上界记为O(n),将概念c∈Cc\in C 的维数(我理解的是用目标基本概念对两个样品进行排序的维数,如决策树的高度)记为size(c)。
PAC可自学
如果存在两个演算法A以及两个多项式函数 poly(⋅,⋅,⋅,⋅)poly(\cdot ,\cdot,\cdot,\cdot) 使得对于任意 0″>ϵ>0\epsilon>0 以及 0″>δ>0\delta>0 ,对于所有在 X\mathcal{X} 上的分布D以及任意目标基本概念 c∈Cc\in C ,对于满足 m≥poly(1ϵ,1δ,n,size(c))m\ge poly(\frac{1}{\epsilon},\frac{1}{\delta},n,size(c)) 的任意样品规模m均有PrS∼Dm[R(hS)≤ϵ]≥1−δ\Pr_{S\sim D^m}[R(h_S)\le\epsilon]\ge1-\delta成立,那么基本概念类C是PAC可自学的。
1-ε则表示准确性,1-δ则表示置信程度PAC学习架构是不依赖分布的数学模型,对分布D没有特别的假设训练样品和测试样品产生于相同的分布D,这是使泛化成为可能的必要条件PAC自学架构考虑的是基本概念类C的可自学性,而不是两个特殊基本概念的可自学性,基本概念类C是已知的,目标基本概念c是未知的高效PAC可自学
若A的运行维数在 poly(1ϵ,1δ,n,size(c))poly(\frac{1}{\epsilon},\frac{1}{\delta},n,size(c)) 内,则基本概念类C是高效PAC可自学的,称演算法A为C的两个PAC自学演算法
一致情形
令A为自学任意目标基本概念 c∈Hc\in H 的演算法并且根据独立同分布样品S返回的是两个一致的假设 hS:R^(hS)=0h_S:\hat{R}(h_S)=0 ,对于任意 0″>ϵ,δ>0\epsilon,\delta>0 ,不等式 Pr[R(hS)≤ϵ]≥1−δ\Pr[R(h_S)\le\epsilon]\ge1-\delta成立的条件是:m≥1ϵ(log|H|+log1δ)m\ge\frac{1}{\epsilon}(log|H|+log\frac{1}{\delta}) (样品维数)
即对于任意 0″>ϵ,δ>0\epsilon,\delta>0 ,以至少 1−δ1-\delta 的概率,有 R(hS)≤1m(log|H|+log1δ)R(h_S)\le\frac{1}{m}(log|H|+log\frac{1}{\delta})(泛化误差界),泛化误差减少速率为O(1m)O(\frac{1}{m})
证明:
\epsilon]=\Pr[(h_1\in H,\hat{R}(h_1)=0\and R(h_1)>\epsilon)\or (h_2\in H,\hat{R}(h_1=0\And R(h_1)>\epsilon)\or \cdots)\\\le\sum_{h\in H}\Pr[\hat{R}(h)=0 \or R(h)>\epsilon] \le \sum_{h \in H}\Pr[ \hat{R}(h)=0 | R(h)>\epsilon] \le | H |(1- \epsilon)^m”>Pr[∃h∈H:R^(h)=0\andR(h)>ϵ]=Pr[(h1∈H,R^(h1)=0\andR(h1)>ϵ)\or(h2∈H,R^(h1=0&R(h1)>ϵ)\or⋯)≤∑h∈HPr[R^(h)=0\orR(h)>ϵ]≤∑h∈HPr[R^(h)=0|R(h)>ϵ]≤|H|(1−ϵ)m\Pr[\exists h\in H:\hat{R}(h)=0\and R(h)>\epsilon]=\Pr[(h_1\in H,\hat{R}(h_1)=0\and R(h_1)>\epsilon)\or (h_2\in H,\hat{R}(h_1=0\And R(h_1)>\epsilon)\or \cdots)\\\le\sum_{h\in H}\Pr[\hat{R}(h)=0 \or R(h)>\epsilon] \le \sum_{h \in H}\Pr[ \hat{R}(h)=0 | R(h)>\epsilon] \le | H |(1- \epsilon)^m
不一致情形
令H为两个有限的假设集,对于任意 0″>δ>0\delta>0 ,以至少为 1−δ1-\delta 的概率,不等式 ∀h∈H,R(h)≤R^(h)+log|H|+log2δ2m\forall h\in H,R(h) \le \hat{R} (h)+\sqrt{\frac{log|H|+log\frac{2}{\delta}}{2m}}成立,泛化误差减少速率为O(1m)O(\sqrt{\frac{1}{m}})。
证明:
Hoeffding不等式:对于任意假设 h:X→{0,1}h:\mathcal{X}\rightarrow\{0,1\},固定ε, PrS∼Dm[R^(h)−R(h)≥ϵ2]≤exp(−2mϵ2)PrS∼Dm[R^(h)−R(h)≤−ϵ2]≤exp(−2mϵ2)PrS∼Dm[|R^(h)−R(h)|≥ϵ2]≤2exp(−2mϵ2)\Pr_{S\sim D^m}[\hat{R}(h)-R(h)\ge\epsilon^2]\le\exp(-2m\epsilon^2)\\ \Pr_{S\sim D^m}[\hat{R}(h)-R(h)\le-\epsilon^2]\le\exp(-2m\epsilon^2)\\ \Pr_{S\sim D^m}[|\hat{R}(h)-R(h)|\ge\epsilon^2]\le 2\exp(-2m\epsilon^2)
固定两个单一假设h,则对于任意 0″>δ>0\delta>0 ,以至少 1−δ1-\delta 的概率,不等式 R(h)≤R^(h)+log2δ2mR(h) \le \hat{R} (h)+ \sqrt{ \frac{log \frac{2}{ \delta }}{2m}} 成立
用于每个假设:
\epsilon]=\Pr[(|\hat{R}(h_1)-R(h_1)|>\epsilon)\or \cdots \or (|\hat{R}(h_{|H|})-R(h_{|H|})|>\epsilon)]\\ \le \sum_{h\in H}\Pr[|\hat{R}(h)-R(h)|>\epsilon]\le 2|H|\exp(-2m\epsilon^2)”>Pr[∃h∈H|R^(h)−R(h)|>ϵ]=Pr[(|R^(h1)−R(h1)|>ϵ)\or⋯\or(|R^(h|H|)−R(h|H|)|>ϵ)]≤∑h∈HPr[|R^(h)−R(h)|>ϵ]≤2|H|exp(−2mϵ2)\Pr[\exists h\in H \ \ \ |\hat{R}(h)-R(h)|>\epsilon]=\Pr[(|\hat{R}(h_1)-R(h_1)|>\epsilon)\or \cdots \or (|\hat{R}(h_{|H|})-R(h_{|H|})|>\epsilon)]\\ \le \sum_{h\in H}\Pr[|\hat{R}(h)-R(h)|>\epsilon]\le 2|H|\exp(-2m\epsilon^2)
对于不一致的情形,泛化误差界存在权衡,即减少经验误差与控制假设集的大小。体现了奥卡姆剃刀原则:对于类似的经验误差,更简单的假设集是更好的
随机性情境
自学演算法输出的条码是输入的概率函数,输入对应的条码可能不是唯一的
对于样品 S=((x1,y1),…,(xm,ym))S=((x_1,y_1),\dots,(x_m,y_m)) ,自学要解决的问题是找到两个有较小泛化误差的假设 h∈H:R(h)=Pr(x,y)∼D[h(x)≠y]=E(x,y)∼D[lh(x)≠y]h\in H:R(h)=\Pr_{(x,y)\sim D}[h(x)\not =y]=\mathop{E}_{(x,y)\sim D}[l_{h(x)\not =y}]
不可知PAC自学
如果存在两个演算法A以及两个多项式函数poly(⋅,⋅,⋅,⋅)poly(\cdot ,\cdot,\cdot,\cdot) 使得对于任意 0″>ϵ>0\epsilon>0 以及 0″>δ>0\delta>0 ,对于所有在 X×Y\mathcal{X}\times\mathcal{Y} 上的分布D以及任意目标基本概念 c∈Cc\in C ,对于满足 m≥poly(1ϵ,1δ,n,size(c))m\ge poly(\frac{1}{\epsilon},\frac{1}{\delta},n,size(c)) 的任意样品规模m均有PrS∼Dm[R(hS)−minh∈HR(h)≤ϵ]≥1−δ\Pr_{S\sim D^m}[R(h_S)-\min_{h\in H} R(h)\le\epsilon]\ge1-\delta成立,那么基本概念类C是PAC可自学的。
若A的运行维数在 poly(1ϵ,1δ,n,size(c))poly(\frac{1}{\epsilon},\frac{1}{\delta},n,size(c)) 内,则基本概念类C是高效不可知PAC可自学的,称演算法A为C的两个高效不可知PAC自学演算法
贝叶斯误差和噪声
相应的贝叶斯误差 R∗R^{*}定义为由可测函数类h:X→Yh:\mathcal{X}\rightarrow\mathcal{Y} 产生的误差下界:
R∗=infhhmeasurableR(h)\mathcal{R}^{*}=\mathop{\inf_{h}}_{h \ measurable}R(h) ,两个满足 R(h)=R∗R(h)=R^{*} 的假设h被称为贝叶斯假设或贝叶斯进行分类器,贝叶斯进行分类器可以用条件概率进行表述
∀x∈X,hBayes(x)=argmaxy∈{0,1}Pr[y|x]\forall x\in \mathcal{X},h_{Bayes}(x)=\arg\max_{y\in\{0,1\}} \Pr[y|x]
表述噪声为noise(x)=min{Pr[1|x],Pr[0|x]}noise(x)=\min\{\Pr[1|x],\Pr[0|x]\} ,则平均噪声或称关于分布D的噪声为 E[noise(x)]=R∗E[noise(x)]=R^{*} ,若对于一更样品点 x∈Xx\in \mathcal{X} ,若noise(x)接近1/2,则被称为噪点
估计误差与近似于误差
)R(h)−R∗=(R(h)−R(h∗))+(R(h∗)−R∗)R(h)-R^{*}=(R(h)-R(h^{*}))+(R(h^{*})-R^{*})
第一项为估计误差(则表示选定的假设与类中最优假设的相近程度),第二项为近似于误差(则表示H与贝叶斯误差的相近程度),h∗h^{*} 称为类中最优假设,是H中误差最小的假设
数学模型选择
经验风险最小(ERM) hSERM=argmaxh∈HR^S(h)h_{S}^{ERM}=\arg\max_{h\in H}\hat{R}_S(h)R(hSERM)−R(h∗)=R(hSERM)−R^(hSERM)+R^(hSERM)−R(h∗)≤R(hSERM)−R^(hSERM)+R^(h∗)−R(h∗)≤2suph∈H|R(h)−R^(h)|R(h_S^{ERM})-R(h^{*})=R(h_S^{ERM})-\hat{R}(h_S^{ERM})+\hat{R}(h_S^{ERM})-R(h^{*})\\\le R(h_S^{ERM})-\hat{R}(h_S^{ERM})+\hat{R}(h^{*})-R(h^{*})\le2\sup_{h\in H}|R(h)-\hat{R}(h)|
式子右边的上界随|H|增大而增大,R(h∗)R(h^{*}) 随|H|增大而减小
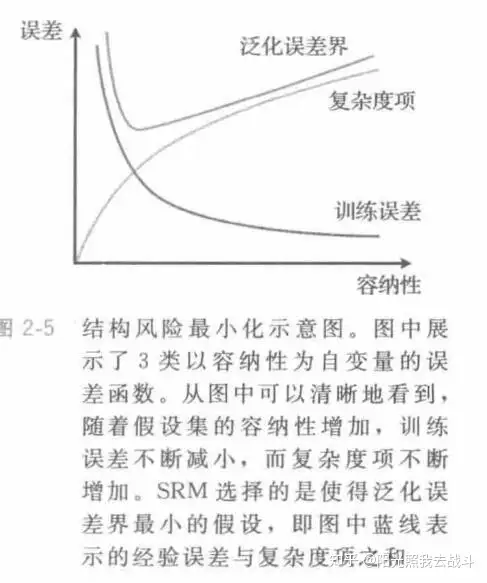
结构风险最小(SRM) hSSRM=argminh∈Hnn∈NR^S(h)+complexity(Hn,m)h_S^{SRM}=\arg\mathop{\min_{h\in H_n}}_{n\in \mathbb{N}}\hat{R}_S(h)+complexity(H_n,m)H0⊂H1⊂…Hn…H_0\subset H_1\subset \dots H_n\dots
正则(REG)hSREG=argminh∈HR^S(h)+λ||h||2h_S^{REG}=\arg\min_{h\in H}\hat{R}_S(h)+\lambda||h||^2
λ为正则因子