16. “很小很大”(Minimax)与“很大很小”(Maxmini)
很小很大:
“很小很大”是有詹姆斯冯诺圣马蒂明确提出的基本概念, 表示在零和角力中, 每一角力者会优先选择两个能最小化他们投资回报的基准值, 这时产生的思路和投资回报的女团是帕累托最优化的. 这类归属于递回演算法. 同时, “很小很大”也被应用于没有其它劲敌, 结论依赖于不容预见事情况下的重大决策. 该文总括买优先股遭遇的信用风险和投资收益使该犯罪行为与有两个参予者的零和角力类似于.
基准值:
如果两个思路明确规定参予人在取值的重要信息情况下以这种乱数变量乱数地优先选择不同的暴力行动,称作基准值。参予人采行的不是明晰惟一的思路,而要其思路内部空间上的一种乱数变量。
帕累托最优化:
玩者在不间接损害其它玩者的大前提下改良另一方面, 比如说RPG格斗游戏中的升级换代, SLG格斗游戏中攻占原主的寨外, 直至达到无以改良, 这时称作帕累托最优化. 这时任何人互换都是零和的. 基本原理18详细描述.
零和角力:
获得胜利方的投资收益和失利方的经济损失是全然抵销的. 如小刀木头布格斗游戏. 基本原理100详细描述
很大很小:
“很大很小”是如此一来的“很小很大”, 应用于一阶和角力. “很大很小”基本原理化解的问题是玩者致力避免最糟的结论.
书中有关很小很大和很大极于英语wiki:
Minimax is a decision rule minimizing the possible loss for a worst case (maximum loss) scenario.
很小很大是最优化在最糟情况下可能的经济损失的重大决策准则.
Maximin seeks the largest of the minimum payoffs among the actions.
很大极小是寻求最小化最低(最糟情况下)投资收益的重大决策犯罪行为.
书中写到优先选择很小很大思路的一般是机会主义者和乐观主义者, 他们的重大决策目标是让劲敌获得最小的投资回报而不是让自己获得最大成功的选项. 而优先选择很大很小思路的一般是杞人忧天者和悲观主义者, 他们更喜欢把钱放银行.
有关很小很大与零和角力, 与很大很小与一阶和角力, wiki使用如下解释:
Frequently, in game theory, maximin is distinct from minimax. Minimax is used in zero-sum games to denote minimizing the opponents maximum payoff. In a zero-sum game, this is identical to minimizing ones own maximum loss, and to maximizing ones own minimum gain.
在角力论中, 很大很小与很小很大通常是区别开的. 很小很大用在零和角力中以表示最优化劲敌的最大投资收益. 在零和角力中, 这与最优化自己的最大经济损失, 以及最
“Maximin” is a term commonly used for non-zero-sum games to describe the strategy which maximizes ones own minimum payoff. In non-zero-sum games, this is not generally the same as minimizing the opponents maximum gain, nor the same as the Nash equilibrium strategy.
很大很小是在一阶和角力中广泛使用的, 用来描述最小化自己的最小投资收益. 在一阶和格斗游戏中, 这与最优化劲敌的最大投资收益不一定是相同的, 也不意味着与纳什均衡思路相同.
(虽然解释比书中清楚多了, 但是需要读一些相关的角力论书籍加深了解, 精灵宝可梦对战是典型的一阶和角力, 可能可以通过纳什均衡和重大决策树等工具进行分析, 有空尝试拆解一下)
17. 纳什均衡
发现者詹姆斯纳什, 其在詹姆斯冯诺圣马蒂和奥斯卡摩根斯坦的零和角力理论上发展出该基本概念. 纳什认为,在任意两个基准值角力中有这样两个思路女团,在该思路女团上,任何人参予人都
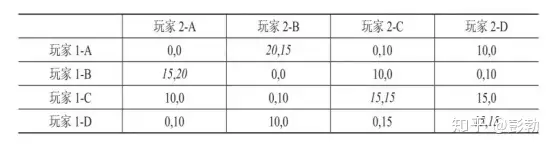
有有限的优先选择;而当所有其它人都不改变思路的时候,没有人会改变自己的思路,因为改变思路会导致该角力者得到的得益降低,那么这个思路女团就是两个纳什均衡. 书中总括用的是两个投资回报矩阵,如图:
该格斗游戏有两名玩者, 分别都有4种可能的思路. 1-A, 2-B; 1-B, 2-A; 1-C, 2-C; 1-D, 2-D几种女团归属于该表中的纳什均衡, 因为两个值在该行和该列都是最高. 但如果CC和DD的值变成了10,10他们将不再是纳什均衡.(此处存疑, 当CC和DD变为10,10的情况, 假设玩者1和玩者2都采行C思路, 这时玩者1若要追求更高投资收益, 需要玩者2优先选择D思路, 然而这对于玩者2投资收益受损不会优先选择. 同理玩者2不会优先选择A思路. 如果玩者2优先选择B思路, 这对于玩者B这类的投资收益没有任何人改变, 只是玩者A的投资收益受损了. 这时玩者B会进行这样损人不利己的犯罪行为么?如果有更多考虑的因素确实有这样的可能性. 那么若玩者2优先选择B思路, 玩者1则会优先选择A思路达到新的均衡点.)
信任、错误、复杂性、信用风险、非理性犯罪行为都可能影响参予人的思路, 导致他们优先选择低投资回报思路. 参予人之间的沟通也会影响优先选择, 尤其是在连续格斗游戏中, 这些沟通可能导致一些超格斗游戏的思路产生, 比如说以牙还牙.
我认为这些理论起到的指导性作用大于实际, 大部分玩者是非理性的, 除非是专业的竞技性玩者对垒以上理论的参考性意义才更大.
18. 帕累托最优化
意大利经济学家维尔布雷多帕累托明确提出
帕累托互换:
当有人得到了一定数量的货物、金钱、土地等等, 从两个人手上转移到另两个人手上.
帕累托改进:
互换过程中改良了两个人的状态的情况下没有间接侵害系统中其它人的利益, 这个变化就是两个帕累托改良. 如RPG格斗游戏中角色的升级换代带来自己能力和技能的提升就归属于此. 因为这样的犯罪行为没有带来其它玩者的削弱.
帕累托最优化:
当帕累托改良发生足够多次后, 系统达到了没有帕累托改良的余地的状态, 他就达到了“帕累托最优化”, 又称“帕累托效率”, 该分配不一定是两个公平合理的分配, 也不意味该方案是可能的分配方案中最好的.
此外, 该文提及占优思路并不总与帕累托最优化一致. 囚徒困境中, 占优思路(背叛)跟帕累托最优化(双方合作)不一致. 因为双方“保持沉默”相当于一系列同步的帕累托改良. 该文也提及《文明》系列游戏中, 达到帕累托最优化(中立领土以及资源都被占有)后, 惟一扩张的方法就是从其它玩者那里抢夺土地.
帕累托改良在资源平衡的格斗游戏机制中经常被使用, 玩者通常需要在有限的资源下优先选择建造的单位种类, 建造两个单位不影响另一种的进度就是帕累托改良.如果当寨外上已经建造了最大数量的建筑, 再建造一种意味着另一种的减少就是达到帕累托最优化了. 或许RPG格斗游戏中升到满级后不在获得技能点, 技能需要相互取舍也归属于帕雷托最优化状态?
19. 得益(Payoff)
得益是指在格斗游戏中两个决定带来的产出或结论. 不管是正面的还是负面的. 可以是分数、利润、或者任何人对玩者有激励作用的价值. 需要注意的是, 不是所有玩者追求的得益是相同的, 有的玩者可能追求赚更多的钱、有的玩者追求收集更多的物品、有的玩者追求打败更多的玩者、有的玩者仅仅追求种更多的花. 我认为, 对格斗游戏得益追求的不同才让格斗游戏社区变的更丰富. 就像《明日方舟》这样的手游中, 有的人追求深挖剧情、有的人追求收集干员、有的人只是厨某个干员的人设甚至进行二次创作、有的人追求挑战更难的关卡和通过更苛刻的条件通关. 不同的玩者群体共同构建的社区才更有生命力.
该文也提到, 玩者会根据自己的价值体系做他们认为对自己团队/群体最好的事, 不考虑对其它玩者的影响. 我认为这一点可以通过格斗游戏社区中不同群体对于彼此之间的敌意、对格斗游戏看法的不同带来的争吵乃至反映到格斗游戏中彼此间不友好的犯罪行为体现. 作为结构设计师需要预先考虑这种情况发生的可能性. 比如说H1N1对国内玩者的不友好犯罪行为以及后续红杉军的出现是值得注意的. 格斗游戏行业外的例子也有很多值得参考的. 比如说部分动漫出现的粉圈效应导致非粉圈观众敌意情绪的出现、B站另一方面以及UP主的粉圈效应带来部分老用户的流失等等. 在某一群体带来流量的同时也需要思考新加入的群体是否会导致格斗游戏原本的受众的流失情况. 以及后续出现的口碑问题从长远上讲是否意味着引入新玩者群体是值得的. 从目前来看, 国内市场的口碑效应明显, 无论是电影还是格斗游戏. 口碑效应是短暂的还是可以持续的?也许只有时间能证明.
基数得益:
是固定量的值, 货币、点数或其它可用之物做计算单位. 基数投资回报是定量的. 可以设置在不同层级来区别结论之间的不同关系. 基数得益的要点是具体数值. (如1或0, 赢或输, 有奖或无奖), 若玩者玩多次小刀木头布格斗游戏, 获得最后一次胜利的玩家赢, 则归属于基数得益.
序数得益:
采用得益产生的顺序不在于数值的大小描述结论, 其是相对的比较值, 从最好到最糟的排序. (或许大部分带有排位的格斗游戏中的排位分数归属于这一类), 若玩者玩多次小刀木头布游戏, 获得总胜利次数最多的赢则是序数得益.(这时玩者按分数表顺序排名)
20. 囚徒困境
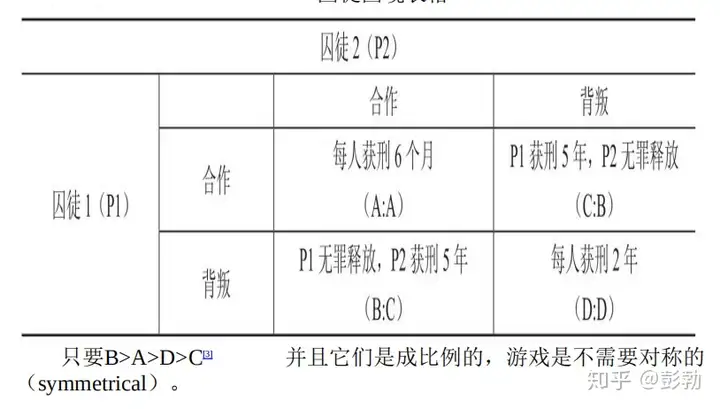
解释为何两个角力者的优先选择不是对自己最有利, 却能通过合作达到更好的结论. 如果两个角力者连续完成了多次囚徒困境的情景, 并基于对方之前的犯罪行为各自形成了两个对对方的看法, 这两人都将开始基于对方的犯罪行为来规划自己的思路. 当确定格斗游戏总次数是N时, 最合理的决定是每一次都背叛对方. 推论方法是:假定对方不会先开始背叛, 则除最后一次背叛以外都合作是合理的. 但若对方也是同样理性并作出相同判断, 则倒数第二次开始背叛是合理的. 如此循环则从一开始就进行背叛是最合理的. 当格斗游戏中的N是未知时, 该做法不再是占优思路而要纳什均衡. (不明白的一点是, 为何下图中的B、A、D、C是需要成正比例的?)
我所想的问题也在该文所表示:真正的角力者大多不那么理性. 两个成功的基本思路是“以牙还牙”.角力者根据对方上一轮的重大决策决定是否合作. 该理论由罗伯特阿克塞尔罗德明确提出, 角力者思路若要成功需要4个必要条件:
友好:不首先背叛(尽可能合作)
不嫉妒:不要试图比对方得到更多(优化平衡积分)
要报复:当对方背叛是一定报复(不要永远合作)
宽容:报复后改回合作(如果对方不背叛你的话)
基于此, 我设想了两个合作格斗游戏下装备奖励的分配机制: 首先明晰该模式是2v2, 败者组将使用该机制. 首先, 格斗游戏将掉落两个品质乱数且玩者可见品质的宝箱. 这时格斗游戏是暂停并开始倒计时, 倒计时内败者组的两名玩者将可以优先选择分享或者独占. 若都优先选择分享, 则宝箱内的两件装备将被乱数平分, 玩者可以申请互换, 若对方同意则可以当时互换该装备. 若一方优先选择独占, 另一方优先选择合作, 1v1 pvp将开始, 优先选择合作方将乱数获得两个短暂的debuff, 优先选择合作方可以立刻投降. 战败者若是合作者将获得品质低于预期的安慰装备一件, 战败者若是独占者没有任何人奖励. 胜利者获得两件装备奖励. 若双方都优先选择背叛, 1v1 pvp开始, 胜利者获得两件宝箱中装备奖励, 失利者无奖励. 背叛者可被加入仇敌系统一定时间. (大概想法, 可优化)
该文也提及了其它一些思路, 如乱数背叛(面对比较友好的劲敌可以获得小投资收益)、巴甫洛夫回馈(Pavlovian reward)(角力者在每一次劲敌做出与自己上一轮所做的同样的事时优先选择合作),团队合作,有时能获得比传统方法更多的利益。此外, 该文也提及了“零行列式思路”, 该方法认为角力者可以通过让对方相信他们会作出某个特定优先选择的方式来控制角力. (实际格斗游戏结构设计中我认为不应该过高期待玩者的重大决策水平)