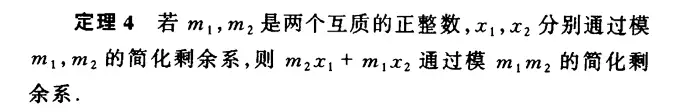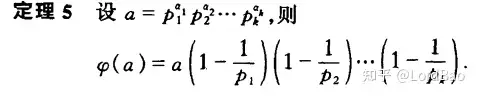【初等数论(闵嗣鹤、严士健)笔记】3.3简化剩余系与欧拉函数

3.3.0序言

上四节：3.2余下类和全然余下系

下四节：3.4笛卡儿不等式.庞加莱不等式或其对无理数的应用领域

沙朗通数学分析大部份讲义收录于在：沙朗通数学分析(闵嗣鹤、严士健)讲义产品目录。

责任编辑将深入探讨两个全然余下系中与模m无理数的有理数，并引入笛卡儿表达式和精简余下系等基本概念。

3.3.1节录

笛卡儿表达式表述

笛卡儿表达式具备如下表所示物理性质:

1. $φ(1)=1,φ(2)=1$ \varphi(1)=1,\varphi(2)=1。2 \iff \varphi(n) \ge 2″> $n>2⟺φ(n)\geq2$ n > 2 \iff \varphi(n) \ge 2。

请看两个常用的推论:

0只与1无理数，0与其它非1有理数均不无理数。

(1,n)=1

(1,n)=1。

(n,n-1)=1

(n,n-1)=1。当n为-1或0或1时，推论显然成立。当

n\leq-2

n \le -2时，

(n,n-1)=(|n-1|,|n|)

(n,n-1)=(|n-1|,|n|),而

|n-1|=|n|+1

|n-1|=|n|+1,根据带余数除法有

(|n-1|,|n|)=(|n|,1)=1

(|n-1|,|n|)=(|n|,1)=1。当

n\geq2

n \ge 2时，由带余数除法可得，

n=n-1+1

n=n-1+1,那么

(n,n-1)=(n-1,1)=1

(n,n-1)=(n-1,1)=1。

由此可得，当2″> $n>2$ n>2时， $n-1\neq1$ n-1 \ne 1,那么至少有 $(n,n-1)=1$ (n,n-1)=1和 $(n,1)=1$ (n,1)=1成立。因此当 2″> $n>2$ n > 2时，有 $φ(n)\geq2$ \varphi(n) \ge 2。反过来，当 $φ(n)\geq2$ \varphi(n) \ge 2时，必然有2″> $n>2$ n>2。

2.若p为质数，那么 $φ(p)=p-1$ \varphi(p)=p-1。

这个证明不难,因为p是质数时，对于两个有理数a而言，要么 $(a,p)=1$ (a,p)=1,要么 $p|a$ p|a。但对于有理数 $0,1,\dots,p-1$ 0,1,\dots,p-1而言，只有 $p|0$ p|0，因此 $φ(p)=p-1$ \varphi(p)=p-1。

3.若p为质数,那么 $φ(pn)=pn-pn-1=pn-1(p-1)$ \varphi(p^n)=p^n-p^{n-1}=p^{n-1}(p-1)。其中n为正有理数。

考虑两个有理数a，则 $(pn,a)=1⟺(p,a)=1$ (p^n,a)=1 \iff (p,a)=1。

证明:

一方面, $(p,a)=1⟹(pn,a)=1$ (p,a)=1 \implies(p^n,a)=1。

另一方面， $(pn,a)=1$ (p^n,a)=1,则 $pn$ p^n的任意因数与a无理数，则 $(p,a)=1$ (p,a)=1.

而 $(pn,a)=1⟺(p,a)=1$ (p^n,a)=1 \iff (p,a)=1等同于 $\neg(pn,a)=1⟺\neg(p,a)=1$ \neg(p^n,a)=1 \iff \neg (p,a)=1。

也即是说若 $a$ a不与 $pn$ p^n无理数当且仅当 $a$ a不与p无理数,又因为p是质数，所以 $a$ a不与p无理数等价于p整除a。

在有理数 $0,1,\dots,pn-1$ 0,1,\dots,p^n-1内能够被p整除的数有 $0p,1p,\dots,xp$ 0p,1p,\dots,xp。而 $xp \le p^n-1 \iff xp <span class=$ x <p^{n-1},即 $x\leqpn-1-1$ x \le p^{n-1}-1。

那么可以得到在 $0,1,\dots,pn-1$ 0,1,\dots,p^n-1内能够被p整除的数有 $pn-1$ p^{n-1}个，那么在 $0,1,\dots,pn-1$ 0,1,\dots,p^n-1内与 $pn$ p^n无理数的数有 $pn-pn-1=pn-1(p-1)$ p^n-p^{n-1}=p^{n-1}(p-1)个。

这里有点绕，好好想一下。

4.笛卡儿表达式并不是单调表达式。

举反例: $φ(5)=4,φ(6)=2$ \varphi(5)=4,\varphi(6)=2。

不等式1(1):

考虑有理数a，模为m，并设a所属的余下类是 $K$ K,那么 $(a,m)=1⟺\forallb\inK, s.t (b,m)=1$ (a,m)=1 \iff \forall b \in K,\text{ s.t }(b,m)=1。

证明:

一方面，由于 $a,b\inK$ a,b \in K,则 $a\equivb(modm)$ a \equiv b \pmod{m},即 $a=mt1+r;b=mt2+r$ a=mt_1+r;b=mt_2+r，那么可以得到 $(b,m)=(m,r)=(a,m)=1$ (b,m)=(m,r)=(a,m)=1。

另一方面，若 $\forallb\inK, s.t (b,m)=1$ \forall b \in K,\text{ s.t }(b,m)=1,显然 $(a,m)=1$ (a,m)=1。

注意：考虑有理数a，模为m，并设a所属的余下类是 $K$ K,那么 $(a,m)=d⟺\forallb\inK, s.t (b,m)=d$ (a,m)=d \iff \forall b \in K,\text{ s.t }(b,m)=d。也是成立的，你看证明过程就知道了。这里将d取1是为了引入精简余下系的基本概念。

无理数余下类的表述：

不等式1(2):

与m无理数的余下类总共有 $φ(m)$ \varphi(m)个。

证明:

在 $0,1,\dots,m-1$ 0,1,\dots,m-1中与m无理数的共有 $φ(m)$ \varphi(m)个，那么显然与m无理数的余下类也是 $φ(m)$ \varphi(m)个。

精简余下系的表述:

有时，我们将全然余下系简称为完系，将精简余下系称为缩系。

不等式2

我觉得没必要刻意去证明。

不等式3

证明:

设X是模m的两个精简余下系，那么X的数目为 $φ(m)$ \varphi(m)个，那么 $Y={ax|x\inX}$ Y=\{ax|x\in X\}的数目是 $φ(m)$ \varphi(m)个，其数量等于 $φ(m)$ \varphi(m)。

设 $xi,xj\inX$ x_i,x_j \in X,且 $xi\neqxj$ x_i \ne x_j,那么可以得到 $axi$ ax_i和 $axj$ ax_j对m不同余(这里参见全然余下系的不等式)。

若 $xk\inX$ x_k \in X，根据精简余下系的表述，那么必然 $(xk,m)=1$ (x_k,m)=1,又因为 $(a,m)=1$ (a,m)=1,那么必然有 $(axk,m)=1$ (ax_k,m)=1。

原书证明:

评注:总的来说，想证明某某通过模M的精简余下系，无非要求3个:

数目是正确的。两两不同余（此处可以沿用完系的推论)。与M无理数。

不等式4

这个不等式其实挺难费解的。

为了简便，不妨令 $m1=m,m2=n,x1=x;x2=y$ m_1=m,m_2=n,x_1=x;x_2=y。

证明:

令 $X1$ X_1表示模m的两个完系， $X2$ X_2是 $X1$ X_1下对模m的两个缩系。

令 $Y1$ Y_1表示模n的两个完系， $Y2$ Y_2是 $Y1$ Y_1下对模n的两个缩系。

令 $Z1={z|z=nx+my,x\inX1,y\inY1}$ Z_1=\{z|z=nx+my,x\in X_1,y \in Y_1\}， $Z2={z|z=nx+my,x\inX2,y\inY2}$ Z_2=\{z|z=nx+my,x\in X_2,y \in Y_2\}, $Z3$ Z_3是 $Z1$ Z_1下对mn的缩系。显然 $Z2\subsetZ1;Z3\subsetZ1$ Z_2 \subset Z_1;Z_3 \subset Z_1。

1.我们已然证明(m,n)=1时，若x,y分别通过模m，n的完系，那么nx+my就通过mn的完系。而 $Z2\subsetZ1$ Z_2 \subset Z_1, $Z1$ Z_1是通过mn的两个完系，那么不难得到 $\forallz1,z2\inZ2,z1\neqz2$ \forall z_1,z_2 \in Z_2,z_1\ne z_2,则必然有 $z1$ z_1和 $z2$ z_2对mn不同余。

2.现在证明 $\forallz\inZ2,$ \forall z \in Z_2,有 $(z,mn)=1$ (z,mn)=1。

先介绍引理:若 $(a,b)=d$ (a,b)=d，那么 $(b,bc+a)=(a,b)=d$ (b,bc+a)=(a,b)=d。

证明: $bc+a=b(c)+a$ bc+a=b(c)+a,那么 $(bc+a,b)=(b,a)=d$ (bc+a,b)=(b,a)=d。

当然，我个人觉得还是挺考验眼力劲儿的。

对于任意 $z\inZ2$ z \in Z_2,存在 $x\inX2,y\inY2$ x \in X_2,y \in Y_2,使得 $z=nx+my$ z=nx+my。那么由缩系表述得， $(x,m)=1,(y,n)=1$ (x,m)=1,(y,n)=1，又因为 $(m,n)=1$ (m,n)=1。

那么可得 $(m,nx)=1,(n,my)=1$ (m,nx)=1,(n,my)=1。

那么可得 $(my+nx,m)=(m,nx)=1;(my+nx,n)=(n,my)=1$ (my+nx,m)=(m,nx)=1;(my+nx,n)=(n,my)=1。

那么可得 $(my+nx,mn)=1$ (my+nx,mn)=1,即 $(z,mn)=1$ (z,mn)=1。

3.证明 $φ(m)φ(n)=φ(mn)$ \varphi(m)\varphi(n)=\varphi(mn)或者说 $Z2=Z3$ Z_2=Z_3。

个人感觉这个版块是最难的，我也没太看懂书上想表达的意思，根据自己的理解来写吧。

一方面，证明 $(z,mn)=1$ (z,mn)=1的过程中，我们证明了 $φ(m)φ(n)\leqφ(mn)$ \varphi(m)\varphi(n)\le \varphi(mn)。

由于 $Z2\subsetZ1$ Z_2 \subset Z_1，那么 $Z1$ Z_1中与mn无理数的个数必然是大于等于 $Z2$ Z_2中与mn无理数的个数的。

而 $Z2$ Z_2与mn无理数的个数就是 $Z2$ Z_2集合元素的个数，即 $φ(m)φ(n)$ \varphi(m)\varphi(n)，而 $Z1$ Z_1是两个数量为mn的完系，由笛卡儿表达式和缩系表述可得， $Z1$ Z_1其与mn无理数的个数为 $φ(mn)$ \varphi(mn)，那么可以得到 $φ(m)φ(n)\leqφ(mn)$ \varphi(m)\varphi(n)\le \varphi(mn)。

或者你由表述可以推得 $Z2\subsetZ3$ Z_2 \subset Z_3也行。

另一方面，考虑对于任意 $z\inZ3$ z \in Z_3，必然 $\existsx\inX1,y\inY1$ \exists x \in X_1,y\in Y_1，使得 $z=nx+my$ z=nx+my,

由于 $Z3$ Z_3是缩系，那么必然有 $(z,mn)=1$ (z,mn)=1,则 $(z,m)=1,(z,n)=1$ (z,m)=1,(z,n)=1。

则

(nx+my,m)=1

(nx+my,m)=1,则

(m,nx)=1

(m,nx)=1,则

(m,x)=1

(m,x)=1。类似可得

(n,y)=1

(n,y)=1。

那么可以得到 $x\inX2,y\inY2$ x\in X_2,y \in Y_2,那么 $z\inZ2$ z \in Z_2,所以 $Z3\subsetZ2$ Z_3 \subset Z_2。所以 $φ(mn)\leqφ(m)φ(n)$ \varphi(mn) \le \varphi(m)\varphi(n)。

综上可得 $φ(m)φ(n)=φ(mn)$ \varphi(m)\varphi(n)= \varphi(mn)。

证毕！

推论

由上诉不等式4证明过程可得。

不等式5

证明:

显然 $(piai,pjaj)=1$ (p_i^{a_i},p_j^{a_j})=1(其中 $i\neqj$ i \ne j, $pi,pj$ p_i,p_j均为质数)。

那么

$φ(a)=φ(p1a1)φ(p2a2)\dotsφ(pkak)=p1a1-1(p1-1)p2a2-1(p2-1)\dotspkak-1(pk-1)=a(1-1p1)(1-1p2)\dots(1-1pk)$ \begin{align*} \varphi(a)& =\varphi(p_1^{a_1})\varphi(p_2^{a_2})\dots\varphi(p_k^{a_k})\\ &=p_1^{a_1-1}(p_1-1)p_2^{a_2-1}(p_2-1)\dots p_k^{a_k-1}(p_k-1)\\ &=a(1-\frac{1}{p_1})(1-\frac{1}{p_2})\dots(1-\frac{1}{p_k}) \end{align*} \\

这个不等式就将笛卡儿表达式和标准质因数分解结合起来了，给出了如何求0到a-1内和a无理数的个数的策略。

另外为了精简表示，我们规定

$φ(a)=a\prodp|a(1-1p)$ \varphi(a)=a\displaystyle\prod_{p|a}(1-\frac{1}{p}) \\

其中p为a的标准分解式出现过的大部份质数。

推论:

若 $(m,n)=d$ (m,n)=d，那么 $φ(mn)=dφ(d)φ(m)φ(n)$ \varphi(mn)=\frac{d}{\varphi(d)}\varphi(m)\varphi(n)。

证明:

显然 $φ(mn)=mn\prodp|mn(1-1p);φ(m)=m\prodp|m(1-1p);φ(n)=n\prodp|n(1-1p)$ \varphi(mn)=mn\displaystyle\prod_{p|mn}(1-\frac{1}{p});\varphi(m)=m\displaystyle\prod_{p|m}(1-\frac{1}{p});\varphi(n)=n\displaystyle\prod_{p|n}(1-\frac{1}{p})。p均表示质数。

对于mn的标准质因数分解式出现的质数p而言，它可以分为两种情况:

1. $p|m;p|n$ p|m;p|n,则此时 $p|(m,n)$ p|(m,n)，即 $p|d$ p|d。

2.p只整除m,n中的两个。

注意，由于 $mn=m\timesn$ mn=m\times n,所以p必然有且只有上面两种情况。

如果为了构造 $φ(mn)=φ(m)φ(n)?$ \varphi(mn)=\varphi(m)\varphi(n)?(?是待完善的式子)，。

显然我们需要对情况1进行分析：不难发现，当 $p|m;p|n$ p|m;p|n时，等式右边的多乘了两个 $(1-1p)$ (1-\frac{1}{p}).因此必然要除掉两个 $(1-1p)$ (1-\frac{1}{p})。

经过分析，我们发现 $p|m;p|n⟺p|d$ p|m;p|n \iff p|d，即d的标准分解式的出现过的质数都多算了一遍。

所以将公式修改为 $φ(mn)=φ(m)φ(n)\prodp|d(1-1p)=dφ(d)φ(m)φ(n)$ \varphi(mn)=\frac{\varphi(m)\varphi(n)}{\displaystyle\prod_{p|d}(1-\frac{1}{p})}=\frac{d}{\varphi(d)}\varphi(m)\varphi(n)

3.3.2习题

1题不做。

2题:这道题，太6了呀。

由于 $(a,m)=1$ (a,m)=1,且 $ξ$ \xi通过模m的精简余下系，那么不难得到 $aξ$ a\xi也通过模m的精简余下系。

不妨设 $aξ$ a\xi通过模m的精简余下系为 $X$ X。

则对于 $\forallaxi\inX$ \forall ax_i \in X,有 $ax_i=mt_i+r_i(0\le r_i<span class=$ ax_i=mt_i+r_i(0\le r_i<m),则 $axim=ti+rim$ \frac{ax_i}{m}=t_i+\frac{r_i}{m}，则 $axim=rim$ {\frac{ax_i}{m}}=\frac{r_i}{m}。

则 $\sumξ{aξm}=\sumrrm$ \displaystyle\sum_{\xi}\{\frac{a\xi}{m}\}=\displaystyle\sum_{r}\frac{r}{m}.其中r是0到m-1中满足与m无理数的有理数。

为了证明该题目，我们引入两个引理:

1. $φ(1)=1,φ(2)=1$ \varphi(1)=1,\varphi(2)=1,当2″> $n>2$ n>2时， $φ(n)\geq2$ \varphi(n)\ge 2，且 $φ(n)$ \varphi(n)为偶数。该引理完善了之前谈到过的笛卡儿表达式的物理性质。

我们仅证明当2″> $n>2$ n>2时， $φ(n)$ \varphi(n)为偶数。

接下来对公式 $φ(a)=a\prodp|a(1-1p)=a\prodp|a(p-1p)$ \varphi(a)=a\displaystyle\prod_{p|a}(1-\frac{1}{p})=a\displaystyle\prod_{p|a}(\frac{p-1}{p})展开分析。

若a的标准分解式仅出现质数2，即 $a=2n(n\geq2)$ a=2^n(n \ge 2)时，我们可以得到 $φ(a)=2n12=2n-1$ \varphi(a)=2^n\frac{1}{2}=2^{n-1}。显然此时 $φ(a)$ \varphi(a)是偶数。

若a的标准分解式出现非2的质数时，我们知道非2的质数都是奇数，那么此时 $p-1$ p-1即为偶数。

由于 $φ(a)=a\prodp|ap\prodp|a(p-1)$ \varphi(a)=\frac{a}{\displaystyle\prod_{p|a}p}\displaystyle\prod_{p|a}(p-1)。不难得到 $a\prodp|ap$ \frac{a}{\displaystyle\prod_{p|a}p}是有理数， $\prodp|a(p-1)$ \displaystyle\prod_{p|a}(p-1)是偶数，因此 $φ(a)$ \varphi(a)是偶数。

2.当2″> $n>2$ n>2时，考虑非负有理数全然余下系(即 $0,1,\dots,n-1$ 0,1,\dots,n-1)下的缩系 $X$ X。我们有若 $a\inX$ a \in X,则必然 $n-a\inX$ n-a \in X，其中 $n-a\neqa$ n-a \ne a。

证明:

当 $a\inX$ a\in X，那么 $(a,n)=1$ (a,n)=1,由于 $n-a=n\times1-a$ n-a=n\times1-a，那么可以得到 $(n-a,n)=(n,-a)=(n,a)=1$ (n-a,n)=(n,-a)=(n,a)=1。即 $(n-a,n)=1$ (n-a,n)=1。

假若 $n-a=a$ n-a=a,那么 $n=2a$ n=2a,那么 $(n,a)=a$ (n,a)= a,由于2,n=2a”> $n>2,n=2a$ n>2,n=2a,那么可得1″> $(n,a)=a>1$ (n,a)=a>1,这与前提 $(n,a)=1$ (n,a)=1矛盾。因此只有 $n-a\neqa$ n-a \ne a。

注意:由于缩系是从与n无理数的余下类各挑选两个元素出来构成的集合，如果你不限制缩系的组成的话，上述推论可以修改为:

当2″> $n>2$ n>2时，若a属于与n无理数的两个余下类，那么 $n-a$ n-a必然属于与n无理数的另两个余下类,且 $n-a\neqa$ n-a \ne a.

这里a与n-a可以属于同两个与n无理数的余下类吗？答案是否定的。

采用反证法证明。

证法1

如若不然，则 $a$ a与 $n-a$ n-a对n同余，那么 $n|n-2a$ n|n-2a，那么 $n|2a$ n|2a。

由于 $(n,a)=1$ (n,a)=1,那么可以得到n和a的标准质因数分解式中没有共同的质数，又 $n|2a$ n|2a,则必然 $n|2$ n|2，那么 $n=\pm1,\pm2$ n=\pm1,\pm2。但是由于2″> $n>2$ n>2,所以导出矛盾，所以a和n-a只能属于不同的余下类。

证法2

如若不然，则 $a$ a与 $n-a$ n-a对n同余，那么 $n|n-2a$ n|n-2a，那么 $n|2a$ n|2a。

由于 $(n,a)=1$ (n,a)=1,则必然存数有理数s,t使得 $ns+at=1$ ns+at=1,等式两边乘以 $2$ 2可得 $2ns+2at=2$ 2ns+2at=2。

由于 $n|2n;n|2a$ n|2n;n|2a,那么可得 $n|2$ n|2。

那么 $n=\pm1,\pm2$ n=\pm1,\pm2。但是由于2″> $n>2$ n>2,所以导出矛盾，所以a和n-a只能属于不同的余下类。

书归正传，回到第2题的证明。

假定 $0\le r<span class=$ 0\le n-r<n,使得 $(n-r,n)=1$ (n-r,n)=1。

而 $r+n-rn=1$ \frac{r+n-r}{n}=1，且 $r\neqn-r$ r \ne n-r。

经过分析不难得到，在 $0\le r<span class=$ 0\le r<n中，总共有 $12φ(m)$ \frac{1}{2}\varphi(m)对。

那么 $\sumξ{aξm}=\sumrrm=12φ(m)$ \displaystyle\sum_{\xi}\{\frac{a\xi}{m}\}=\displaystyle\sum_{r}\frac{r}{m}=\frac{1}{2}\varphi(m)

3题:第1问比较简单，故不证。

第2问:Awesome！

第2问应该假定a是正有理数。

令 $a=p1a1p2a2\dotspkak$ a=p_1^{a_1}p_2^{a_2}\dots p_k^{a_k},由第(1问)可得:

$a=(φ(1)+φ(p1)+\dots+φ(p1a1))(φ(1)+φ(p2)+\dots+φ(p2a2))\dots(φ(1)+φ(pk)+\dots+φ(pkak))$ a=\Big(\varphi(1)+\varphi(p_1)+\dots+\varphi(p_1^{a_1})\Big)\Big(\varphi(1)+\varphi(p_2)+\dots+\varphi(p_2^{a_2})\Big)\dots\Big(\varphi(1)+\varphi(p_k)+\dots+\varphi(p_k^{a_k})\Big)

经过发现，其实等式右侧即为占布在a的一切正因数上的和式。

即 $\sumd|aφ(d)=a$ \displaystyle\sum_{d|a}\varphi(d)=a,其中 $\sumd|a$ \displaystyle\sum_{d|a}表示占布在a的一切正因数上的和式。

4题:

由于缩系是完系的子集，而在上节中已然证明完系中的不同余性，故这里不再证明不同余物理性质。

为了方便表示，令 $x=ξ$ x=\xi。

先证明 $(M1x1+M2x2+\dots+Mkxk,m)=1$ (M_1x_1+M_2x_2+\dots+M_kx_k,m)=1。

由题 $m1,m2,\dots,mk$ m_1,m_2,\dots,m_k是k个两两不无理数的有理数，那么可以得到 $(m1,m2m3\dotsmk)=(m1,M1)=1$ (m_1,m_2m_3\dots m_k)=(m_1,M_1)=1。

则可推知 $(mi,Mi)=1(i=1,2,\dots,k)$ (m_i,M_i)=1(i=1,2,\dots,k)。

又因为 $(mi,xi)=1$ (m_i,x_i)=1，那么可以得到 $(mi,Mixi)=1$ (m_i,M_ix_i)=1。

由于 $M1x1+M2x2+\dots+Mkxk=m1(?)+M1x1$ M_1x_1+M_2x_2+\dots+M_kx_k=m_1(?)+M_1x_1,其中 $?$ ?是个有理数，因为 $M2,M3,\dots,Mk$ M_2,M_3,\dots,M_k均含因子 $m1$ m_1。

那么可以得到 $(M1x1+M2x2+\dots+Mkxk,m1)=(m1,M1x1)=1$ (M_1x_1+M_2x_2+\dots+M_kx_k,m_1)=(m_1,M_1x_1)=1。

类似可得 $(M1x1+M2x2+\dots+Mkxk,mi)=1(i=1,2,\dots,k)$ (M_1x_1+M_2x_2+\dots+M_kx_k,m_i)=1(i=1,2,\dots,k)。

那么可以得到 $(M1x1+M2x2+\dots+Mkxk,m)=1$ (M_1x_1+M_2x_2+\dots+M_kx_k,m)=1。

再证明数目一致。

由于m_1,m_2,\dots,m_k是k个两两不无理数的有理数，那么\varphi(m_1m_2\dots m_k)=\varphi(m_1)\varphi(m_2\dots m_k)=\varphi(m_1) \varphi(m_2)\dots \varphi(m_k)。

显然数目是一致的。

3.3.3总结

这四节只有3页，我却花了将近3天来看，还是蛮难的，因为涉及到了许多衍生的推论和不等式。

关于这四节，我觉得需要知道如下表所示东西:

1.笛卡儿表达式的表述和物理性质。

笛卡儿表达式最开始的表述是\varphi(a)为0,1,\dots,a-1上与a无理数的有理数个数。但是到后面接触了无理数余下类之后，我们知道同两个无理数剩余类的元素均与a是无理数的。所以笛卡儿表达式也可以理解为a的无理数余下类个数，或者说是两个完欧佩什县与a无理数的个数。

笛卡儿表达式的物理性质有很多，

当p为质数时，有\varphi(p)=p-1;\varphi(p^n)=p^{n}-p^{n-1}=p^{n-1}(p-1);p^n=\varphi(1)+\varphi(p)+\dots+\varphi(p^{n})\varphi(1)=1,\varphi(2)=1,当2″>n>2时，\varphi(n)\ge 2，且\varphi(n)为偶数。设a=p_1^{a_1}p_2^{a_2}\dots p_k^{a_k},则\varphi(a) =a(1-\frac{1}{p_1})(1-\frac{1}{p_2})\dots(1-\frac{1}{p_k})=a\displaystyle\prod_{p|a}(1-\frac{1}{p})。若(m,n)=d,则\varphi(mn)=\frac{\varphi(m)\varphi(n)}{\displaystyle\prod_{p|d}(1-\frac{1}{p})}=\frac{d}{\varphi(d)}\varphi(m)\varphi(n)。特别地，当(m,n)=1时，有\varphi(mn)=\varphi(m)\varphi(n)。\displaystyle\sum_{d|a}\varphi(d)=a,其中\displaystyle\sum_{d|a}表示占布在a的一切正因数上的和式。笛卡儿表达式并不是单调表达式。

2.两个常用的推论:

0只与1无理数，0与其它非1有理数均不无理数。(1,n)=1。(n,n-1)=1。(a+br,b)=(b,a)。

3.缩系，完系，与模无理数的余下类，余下类之间的关系。

余下类将大部份有理数按照余数的情况化为了m类(m为模的大小)，完系就是从每个余下类中挑选两个元素构成的集合，不难得到完系的个数为m个。常用的完系有最小非负有理数完系，最小绝对值完系。

缩系是从完系中挑选的与模m无理数的元素构成的集合，由于缩系每个元素代表的余下类中的元素均是与模m无理数的，所以将这些余下类称为与模无理数的余下类。在数量上，与模无理数的余下类的个数等于缩系的元素个数，等于\varphi(m)。

4.总的来说，想证明某某通过模M的精简余下系，无非要求3个:

数目是正确的。两两不同余（此处可以沿用完系的推论)。与M无理数。

这里尤其注意的是缩系是完系的子集，如果有现成的完系物理性质，那么不同余的物理性质就可以不必再证明。此外，在引入了那么多的笛卡儿表达式物理性质的时候，初步判断数目上的证明应该不难了。本节课的两个难点就是不等式4的时候，用了一点集合论的知识证明(m,n)=1时，\varphi(mn)=\varphi(m)\varphi(n)。

这里务必记住不等式3，不等式4的内容和其证明过程，建议将习题的4问也记住，因为它本质上就是不等式4的推广。

5.此外，可以记住习题中引入的引理:

1.当2″>n>2时，考虑非负有理数全然余下系(即0,1,\dots,n-1)下的缩系X。我们有若a \in X,则必然n-a \in X，其中n-a \ne a。

2.当2″>n>2时，若a属于与n无理数的两个余下类，那么n-a必然属于与n无理数的另两个余下类,且n-a \ne a

这个习题也可以留意一下: