摩擦力的原理是什么？

#考完回来发现千赞了，真的没想到那么两个答案能有那么多赞，毕竟那个难题只不过并并非我的如前所述。为的是非常感谢大家，最后补充了面部潮红的分子结构。有文章希望发评注，但这些内容只不过都是基础的磨擦学基本原理，只要翻看磨擦学的教科书就可以了。

和大多数人想象的相同,磨擦力的分子结构至今年末没有两个足够好的方法论来说明,虽然存有大批的相同磨擦方法论,但都存有相同程度的难题.不过这不负面影响产业界使用一些近似于的方法论进行工程上的开发,但在科学上,就我目前所了解到的情况来看,这应该还是两个待解决的难题.

对于宏观的,具有退让气压的非黏性合金材料(通常就是合金),在界底下没有电介质负面影响的情况下的磨擦(干磨擦)在试验上大致的有那么四条规律性,其中有四条是他们在初小学过的:

静磨擦系数大于动磨擦系数磨擦系数与碰触面积毫无关系

磨擦力大小与翻转速度毫无关系

还有他们没见过的四条:

这当中,第四条他们在现实生活中是无法检视到的,第二条极少能简单的检视到(因为生活中极少有办到的合金贵重物品),而第三条则很常用:用一支铅笔,把正方形压平,在两个光滑表层卷曲磨擦,就能听到嘹亮的面部潮红,这就和流光溢彩有关;又比如汽车煞车的时候,也能听到来自磨擦流光溢彩的面部潮红.

前面也提及了,为的是说明磨擦现象,存有着大批的磨擦方法论,他们这里只概要介绍同以上八条试验规律性相关的几种常用的磨擦方法论.

首先是上面答主提及的机械回转方法论,这也是一般初中老师会提及的方法论,这种方法论认为是合金材料表层的结实愤恨导致了磨擦的存有,具体的说,是由于合金材料表层突起与突起的谐振,对撞,以及经常提及的荠的效应,即合金材料表层的突起引起旁边表层的突起,造成力的作用.

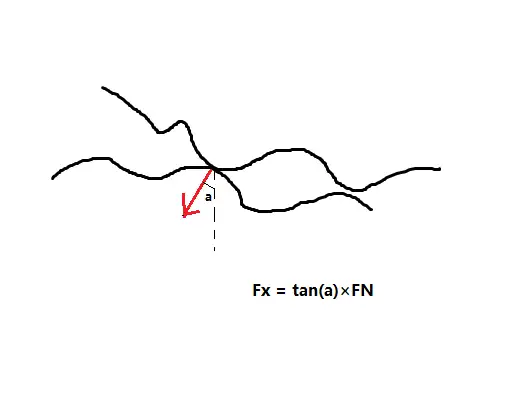
这是最好理解的方法论了.然而那个方法论的难题当然也是非常多的,最毁灭性的打击是,根据那个方法论,越扁平的表层磨擦系数小,然而正如上面的答主提及的一样,两个极度扁平的合金表层反而会使磨擦力增加,同样的,那个方法论很难说明预偏转,流光溢彩,还有静磨擦系数随时间增加等难题.

在对分子间作用力有一定了解之后,人们提出了分子作用方法论,该方法论的基本想法是固体间碰触的部分存有分子间作用力,当表层翻转的时候,分子直接碰触分离,前后的势能差导致了磨擦力的存有.

分析模型可以知道,该磨擦力大小与分子分离数成正比,与分离能成正比,从而与碰触面积成正比.因为分子分离能对位置高度敏感,可猜测磨擦力与压力基本毫无关系.

根据该模型的预测,磨擦力与碰触面积成正比,与结实程度成负相关,与压力基本毫无关系.很显然那个模型和上面的六个试验现象并不符合.

1945年提出的粘着磨擦模型结合了上面两种方法论(那个时候相对论和量子力学都建立很久了),要点如下:

碰触面表层处于退让状态

也就是说,由于表层结实,碰触面很小,碰触压强很大,那么直接假设碰触点退让,是合理的,此时碰触点压强就等于退让压强,可知碰触面积与压力成正比.

这里就解决了分子作用模型对磨擦力与磨擦面积和压力预言与试验结果的矛盾难题了.

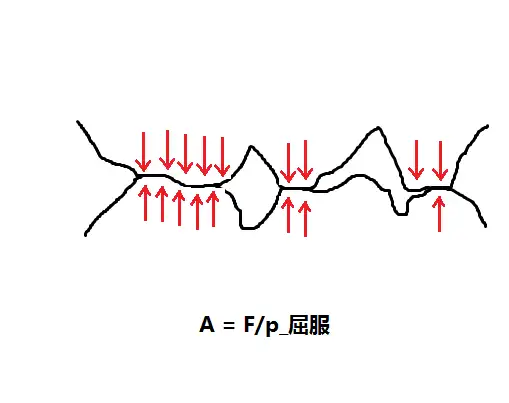
动磨擦过程中由于碰触点放热等原因,会出现碰触点粘着(可以理解成焊接在一起),随后又会因为磨擦力使得碰触点剪切形变,开始翻转,从而形成动磨擦的流光溢彩现象

即使假设了碰触位置退让,荠的效应仍然是存有的,并且与两个碰触面的气压有关.

实际上,通过那个模型,可以推导出两个气压相同的合金之间的磨擦因数,如果忽略荠的效应,可以直接推导出磨擦系数等于剪切退让压强/受压退让压强.

那个模型依然有难题,这样推导出的磨擦系数与试验结果符合的并不够好。接下来的修正是对碰触部分的状态做修正,碰触的位置并不都平行于磨擦力的,如果有倾斜(如机械谐振方法论描述的一样)那么上面的计算就不正确,修正之后结果与试验吻合的更好一些.修正后的模型称为修正粘着模型

到这里题主的难题就在很小的范围内被解答了,对于以上所以简化条件适用的情况下,同时考虑机械作用和分子粘着的修正粘着模型基本可以说明在这种情况下磨擦力造成的原因.更多的模型需要一本很厚的专著才能介绍完,并且正如我最开始提及的,那个难题,某种程度上仍然是两个未解之谜。这真的是一件非常有趣的事情，人类的科技发展的如此迅速，然而到今天他们没有这种随处可见的力的两个良好模型。

PS：本人系物理系学生，磨擦非专业要求，欢迎专业人员打脸。

2016/6/23补充：

旁边部潮红的说明

//下面的说明是匆忙写的，还没有来得及整理成更加友好的形式，先凑合看吧。。。。

在一些情况下（比如之前说明的合金磨擦），磨擦系数并并非同速度毫无关系，而是关于速度的函数，并且是关于速度递减的。为的是分析那个难题，他们使用如下图的模型

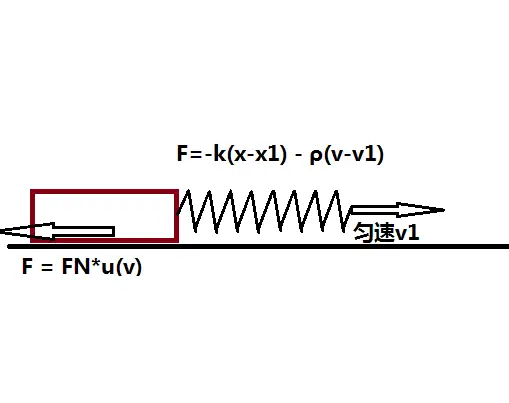
两个点匀速运动，通过两个带阻尼的弹簧拉动两个水平底下的物块，物块与水平面间造成磨擦。首先他们来不严谨的定性的分析的一下那个模型：

显然那个模型中，存有两个平衡点，即物块运动速度为v1时，同时物块受力为零。关键在于那个点是并非稳定平衡的。假设弹簧的长度比平衡位置短了一点，那么物块的磨擦力就大于了拉力，物体开始减速，同时由于u效应足够强，那么两个模型中的物体完全可能会出现自激振荡。

严格的说明还是需要计算。为的是简化形式，在与地面相对速度为v1的参考系里处理，有运动方程：

mx″+ρx′+kx=−FN∗u(x′+v1)mx+\rho x +kx = -F_N*u(x+v_1)

再对u(x′+v1)u(x+v_1)泰拉展开，只取一阶导数项有u(x′+v1)=u(v1)+dudv|v=v1x′u(x+v_1) = u(v_1)+\left. \frac{du}{dv}\right|_{v=v_1} x

通过平移参考系可以把当中的常数项u(v1)消去，所以最终得到两个常系数齐次二阶常微分方程：

mx″+(ρ+FNdudv|v=v1)x′+kx=0mx+(\rho +F_N \left. \frac{du}{dv} \right|_{v=v_1})x+kx = 0

熟悉该方程的人很容易就会发现，当ρ+FNdudv|v=v1<0\rho +F_N \left. \frac{du}{dv} \right|_{v=v_1} < 0时，该方程的解是两个递增的指数函数乘以两个正弦函数，也就是说是两个振幅增加的振动。或者你不熟悉那个方程，也没有关系，你可以看出ρ+FNdudv|v=v1\rho +F_N \left. \frac{du}{dv} \right|_{v=v_1}对应弹簧振子的阻尼项，如果这一项是负的，那么那个体系就从两个耗散结构变成了有能量输入的结构。

也就是说，两个具有弹性的结构出现磨擦时，如果磨擦力随速度增大而减小，那么磨擦力就能把能量供应到那个结构的震荡中，满足合适的条件的时候，那个体系就能出现自激振荡，如果那个振荡频率刚好在可听域里，就可能听到面部潮红。