译者 | 开发人员吴师弟
风险提示十分钟学演算法(ID:CXYxiaowu)
1 结语
结点
是指从某一结点起程,依照很大的的搜寻走线,依序出访对计算机程序中的全数结点,且每一结点仅出访一场。
在链表此基础中,如是说了对树的结点。树的结点是指从根结点起程,依照很大的出访准则,依序出访树的每一结点重要信息。树的结点操作过程,根据出访准则的相同主要就分成三种结点形式:
(1)先序结点
(2)前序结点
(3)结语结点
(4)层级结点
类似于的,图的结点是指,从取值图中任一选定的三角形(称作如上所述点)起程,依照这种搜寻方式沿著图的边出访图中的大部份三角形,使每一三角形仅被出访一场,那个操作过程称作图的结点。结点操作过程中获得的三角形字符串称作图结点字符串
。
图的结点操作过程中,依照搜寻方式的相同,又可以划分成三种搜寻策略:
(1)深度优先搜寻(DFS,Depth First Search)
(2)广度优先搜寻(BFS,Breadth First Search)
2 深度优先搜寻2.1 演算法思想
深度优先搜寻思想:假设如上所述状态是图中大部份三角形均未被出访,则从某一三角形v起程,首先出访该三角形,然后依序从它的各个未被出访的邻接点起程深度优先搜寻结点图,直至图中大部份和v有路径相通的三角形都被出访到。若此时尚有其他三角形未被出访到,则另选一个未被出访的三角形作起始点,重复上述操作过程,直至图中大部份三角形都被出访到为止。
2.2 演算法特点
深度优先搜寻是一个递归的操作过程。首先,选定一个起程点后进行结点,如果有邻接的未被出访过的结点则继续前进。若不能继续前进,则回退一步再前进,若回退一步仍然不能前进,则连续回退至可以前进的位置为止。重复此操作过程,直到大部份与选定点相通的大部份三角形都被结点。
深度优先搜寻是递归操作过程,带有回退操作,因此需要使用栈存储出访的路径重要信息。当出访到的当前三角形没有可以前进的邻接三角形时,需要进行出栈操作,将当前位置回退至出栈元素位置。
2.3 图解操作过程2.3.1 无向图深度优先搜寻
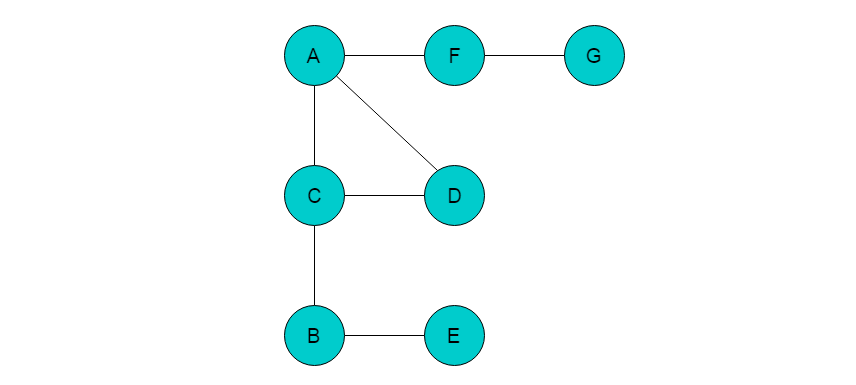
以图2.3.1.1中所示无向图说明深度优先搜寻结点操作过程。
图2.3.1.1
(1)首先选取三角形A为起始点,输出A三角形重要信息,且将A入栈,并标记A为已出访三角形。
(2)A的邻接三角形有C、D、F,从中任一选取一个三角形前进。这里我们选取C三角形为前进位置三角形。输出C三角形重要信息,将C入栈,并标记C为已出访三角形。当前位置指向三角形C。
(3)三角形C的邻接三角形有A、D和B,此时A已经标记为已出访三角形,因此不能继续出访。从B或者D中选取一个三角形前进,这里我们选取B三角形为前进位置三角形。输出B三角形重要信息,将B入栈,标记B三角形为已出访三角形。当前位置指向三角形B。
(4)三角形B的邻接三角形只有C、E,C已被标记,不能继续出访,因此选取E为前进位置三角形,输出E三角形重要信息,将E入栈,标记E三角形,当前位置指向E。
(5)三角形E的邻接三角形均已被标记,此时无法继续前进,则需要进行回退。将当前位置回退至三角形B,回退的同时将E出栈。
(6)三角形B的邻接三角形也均被标记,需要继续回退,当前位置回退至C,回退同时将B出栈。
(7)三角形C可以前进的三角形位置为D,则输出D三角形重要信息,将D入栈,并标记D三角形。当前位置指向三角形D。
(8)三角形D没有前进的三角形位置,因此需要回退操作。将当前位置回退至三角形C,回退同时将D出栈。
(9)三角形C没有前进的三角形位置,继续回退,将当前位置回退至三角形A,回退同时将C出栈。
(10)三角形A前进的三角形位置为F,输出F三角形重要信息,将F入栈,并标记F。将当前位置指向三角形F。
(11)三角形F的前进三角形位置为G,输出G三角形重要信息,将G入栈,并标记G。将当前位置指向三角形G。
(12)三角形G没有前进三角形位置,回退至F。当前位置指向F,回退同时将G出栈。
(13)三角形F没有前进三角形位置,回退至A,当前位置指向A,回退同时将F出栈。
(14)三角形A没有前进三角形位置,继续回退,栈为空,则以A为起始的结点结束。若图中仍有未被出访的三角形,则选取未出访的三角形为起始点,继续执行此操作过程。直至大部份三角形均被出访。
(15)采用深度优先搜寻结点顺序为A->C->B->E->D->F->G。
2.3.2 有向图深度优先搜寻
以图2.3.2.1中所示有向图说明深度优先搜寻结点操作过程。
图2.3.2.1 有向图
(1)以三角形A为起始点,输出A,将A入栈,并标记A。当前位置指向A。
(2)以A为尾的边只有1条,且边的头为三角形B,则前进位置为三角形B,输出B,将B入栈,标记B。当前位置指向B。
(3)三角形B可以前进的位置有C与F,选取F为前进位置,输出F,将F入栈,并标记F。当前位置指向F。
(4)三角形F的前进位置为G,输出G,将G入栈,并标记G。当前位置指向G。
(5)三角形G没有可以前进的位置,则回退至F,将F出栈。当前位置指向F。
(6)三角形F没有可以前进的位置,继续回退至B,将F出栈。当前位置指向B。
(7)三角形B可以前进位置为C和E,选取E,输出E,将E入栈,并标记E。当前位置指向E。
(8)三角形E的前进位置为D,输出D,将D入栈,并标记D。当前位置指向D。
(9)三角形D的前进位置为C,输出C,将C入栈,并标记C。当前位置指向C。
(10)三角形C没有前进位置,进行回退至D,回退同时将C出栈。
(11)继续执行此操作过程,直至栈为空,以A为起始点的结点操作过程结束。若图中仍有未被出访的三角形,则选取未出访的三角形为起始点,继续执行此操作过程。直至大部份三角形均被出访。
2.4 演算法分析
当图采用邻接矩阵存储时,由于矩阵元素个数为n^2,因此时间复杂度就是O(n^2)。
当图采用邻接表存储时,邻接表中只是存储了边结点(e条边,无向图也只是2e个结点),加上表头结点为n(也就是三角形个数),因此时间复杂度为O(n+e)。
3 广度优先搜寻3.1 演算法思想
广度优先搜寻思想:从图中某三角形v起程,在出访了v之后依序出访v的各个未曾出访过的邻接点,然后分别从这些邻接点起程依序出访它们的邻接点,并使得“先被出访的三角形的邻接点先于后被出访的三角形的邻接点被出访,直至图中大部份已被出访的三角形的邻接点都被访问到。如果此时图中尚有三角形未被出访,则需要另选一个未曾被出访过的三角形作为新的起始点,重复上述操作过程,直至图中大部份三角形都被出访到为止。
3.2 演算法特点
广度优先搜寻类似于于树的层级结点,是依照一种由近及远的方式出访图的三角形。在进行广度优先搜寻时需要使用队列存储三角形重要信息。
3.3 图解操作过程
3.3.1 无向图的广度优先搜寻
例如:图3.3.1.1所示的无向图,采用广度优先搜寻操作过程。
图3.3.1.1
(1)选取A为起始点,输出A,A入队列,标记A,当前位置指向A。
(2)队列头为A,A出队列。A的邻接三角形有B、E,输出B和E,将B和E入队,并标记B、E。当前位置指向A。
(3)队列头为B,B出队列。B的邻接三角形有C、D,输出C、D,将C、D入队列,并标记C、D。当前位置指向B。
(4)队列头为E,E出队列。E的邻接三角形有D、F,但是D已经被标记,因此输出F,将F入队列,并标记F。当前位置指向E。
(5)队列头为C,C出队列。C的邻接三角形有B、D,但B、D均被标记。无元素入队列。当前位置指向C。
(6)队列头为D,D出队列。D的邻接三角形有B、C、E,但是B、C、E均被标记,无元素入队列。当前位置指向D。
(7)队列头为F,F出队列。F的邻接三角形有G、H,输出G、H,将G、H入队列,并标记G、H。当前位置指向F。
(8)队列头为G,G出队列。G的邻接三角形有F,但F已被标记,无元素入队列。当前位置指向G。
(9)队列头为H,H出队列。H的邻接三角形有F,但F已被标记,无元素入队列。当前位置指向H。
img
(10)队列空,则以A为起始点的结点结束。若图中仍有未被出访的三角形,则选取未出访的三角形为起始点,继续执行此操作过程。直至大部份三角形均被出访。
3.3.2 有向图的广度优先搜寻
以图3.3.2.1所示的有向图为例进行广度优先搜寻。
图3.3.2.1
(1)选取A为起始点,输出A,将A入队列,标记A。
(2)队列头为A,A出队列。以A为尾的边有两条,对应的头分别为B、C,则A的邻接三角形有B、C。输出B、C,将B、C入队列,并标记B、C。
(3)队列头为B,B出队列。B的邻接三角形为C,C已经被标记,因此无新元素入队列。
(4)队列头为C,C出队列。C的邻接三角形有E、F。输出E、F,将E、F入队列,并标记E、F。
(5)队列头为E,E出队列。E的邻接三角形有G、H。输出G、H,将G、H入队列,并标记G、H。
(6)队列头为F,F出队列。F无邻接三角形。
(7)队列头为G,G出队列。G无邻接三角形。
(8)队列头为H,H出队列。H邻接三角形为E,但是E已被标记,无新元素入队列。
(9)队列为空,以A为起始点的结点操作过程结束,此时图中仍有D未被出访,则以D为起始点继续结点。选取D为起始点,输出D,将D入队列,标记D。
(10)队列头为D,D出队列,D的邻接三角形为B,B已被标记,无新元素入队列。
(11)队列为空,且大部份元素均被出访,广度优先搜寻结点操作过程结束。广度优先搜寻的输出字符串为:A->B->E->C->D->F->G->H。
3.4 演算法分析
假设图有V个三角形,E条边,广度优先搜寻演算法需要搜寻V个结点,时间消耗是O(V),在搜寻操作过程中,又需要依照边来增加队列的长度,于是这里需要消耗O(E),总得来说,效率大约是O(V+E)。
4 总结
图的结点主要就就是这三种结点思想,深度优先搜寻使用递归形式,需要栈结构辅助实现。广度优先搜寻需要使用队列结构辅助实现。在遍历操作过程中可以看出,对连通图,从图的任一一个三角形开始深度或广度优先结点很大可以出访图中的大部份三角形,但对非连通图,从图的任一一个三角形开始深度或广度优先结点并不能出访图中的大部份三角形。
(本文为 AI大本营转载文章,转载请联系原译者)