社交数据那么多，看Facebook如何用贝叶斯实时优化后端

LizierFacebook，作者：Ben Letham、Brian Karrer、Guilherme Ottoni、Eytan Bakshy。机器之心校对。

面对每晚海量统计数据更新的新浪网统计数据，Facebook 要谋求快速的模块强化方式来逐步完善后端控制系统，而分层搜寻和纯手工调参显然不是合适的选择。

Facebook 每晚依赖两套大型后端控制系统服务于数千万人。那些控制系统中大部分都具有大批内部模块，如支持 Facebook 的 web 伺服器采用 HipHop 软件包（HHVM）来满足允诺，HHVM 有十几个模块来控制动态C++。另一各方面，机器学习控制系统可用来执行很多预测任务。那些控制系统一般来说包含预测数学模型的数个层，其中有大批模块，用作下定决心数学模型怎样连接以输出最终推荐。那些模块要通过采用动态的乱数试验来仔细修正，也就是所谓的 A/B 试验。每一试验可能将耗费一周或更长时间，因而症结在于用更少的试验强化两套模块。

A/B 测试一般来说被用作改良产品的纸制试验。在学术论文《Constrained Bayesian Optimization with Noisy Experiments》（也已刊载在《Bayesian Analysis》杂志）中，Facebook 描述了怎样采用一种名叫「可计算性强化」的 AI 控制技术，根据早先试验的结论自适应地设计半程 A/B 试验。与分层搜寻或纯手工调参相比，可计算性强化能用更少的试验联手修正更多的模块，并找到更快的值。Facebook 已经采用该控制技术在一批后端控制系统中展开了十多次调参试验，发现该控制技术在机器学习控制系统调参各方面非常有效。

针对 A/B 试验的可计算性强化

新浪网控制系统调参的众所周知方式是全自动运转较大型分层搜寻来分别强化每一模块。可计算性强化构筑了模块和兴趣新浪网结论间的统计数学模型，并采用该数学模型来下定决心展开什么样试验。此种基于数学模型的方式有几个关键优势，尤其是在强化新浪网机器学习控制系统各方面：

更快地利用模块维度展开翻转：由于运转新浪网试验存有数量限制，分层搜寻或纯手工调参不能用作同时修正数个模块。数学模型的采用使可计算性强化能扩展到更多的模块，一般来说联手强化的模块能达到 20 个。这对机器学习控制系统非常重要，因为在那些控制系统中，模块间经常存有交互作用，需要联手强化。

试验单次减少：可计算性强化使我们能从数轮试验中获得重要信息：连续内部空间中的一次模块值的试验不仅能提供更多有关该试验结论的重要信息，还能提供更多周围点的重要信息。因而，探索内部空间所需的试验单次能大大增加。

试验结论更快：数学模型能辨识内部空间中可能将无法提供更多良好结论的部分，避免在那些模块值上运转试验。此种做法改良了试验组内的经验。

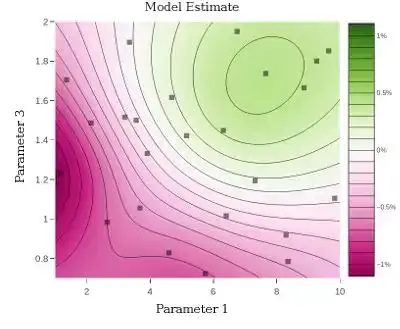
认知模块内部空间：数学模型帮助我们建模并更快地认知模块怎样影响钟爱的结论。右图显示了一个 8 模块试验的三维切碎，是为了更快地认知模块内部空间而展开的建模的众所周知范例：

下文将提供更多可计算性强化的深入介绍，并讨论来自学术论文的工作及其中的一些试验结论。

可计算性强化

可计算性强化是一种解决最强化问题的控制技术，其中未知形式的目标函数（即新浪网度量）不会有解析解，且它只能通过一些耗时的运算（即乱数试验）评估出来。通过有限的试验数高效探索多维内部空间的关键是建模：真实的目标函数是未知的，但是我们能令数学模型拟合已有的观察样本，并采用数学模型预测模块内部空间中更快的部分，而这一部分应该需要运转更多的试验。

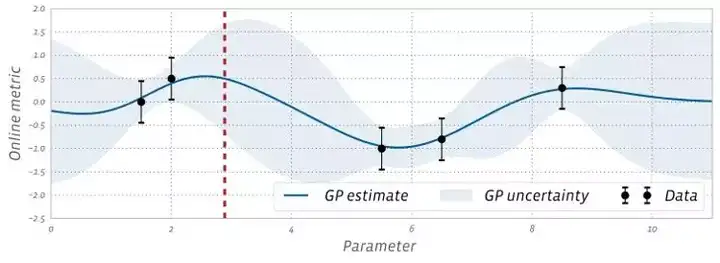
高斯过程（GP）是一种非模块的可计算性数学模型，因为它能提供更多优秀的不确定性估计和简便的分析，所以高斯过程非常适用作可计算性强化。高斯过程为目标函数提供更多了一种估计，它用来判断随着模块的变化新浪网度量到底会怎么变化：

上图中每一个统计数据标记对应于该模块值的 A/B 试验结论。通过平衡探索（很大的不确定性）和利用（良好的数学模型估计），我们能采用高斯过程来下定决心接下来要试验的模块。这一过程能通过计算采集函数（Acquisition Function）完成，该函数用任何给定的模块值来估计执行试验后的观察值。

假设我们正尝试下定决心是否应该采用模块配置 x 执行一次试验，那么在 x 的情况下观察值有多大的价值？这个问题的答案依赖于效用函数。现在假设在观察到 x 后就结束强化，那么那些模块的效用就仅仅只是它所找到的最优解的值。在此种情况下，观察到 x 的效用就是 f(x)，相当于当前最优的改良程度，我们能称为 x*（假设我们在做最大化）：I(x) = max(0, f(x) – f(x*))。

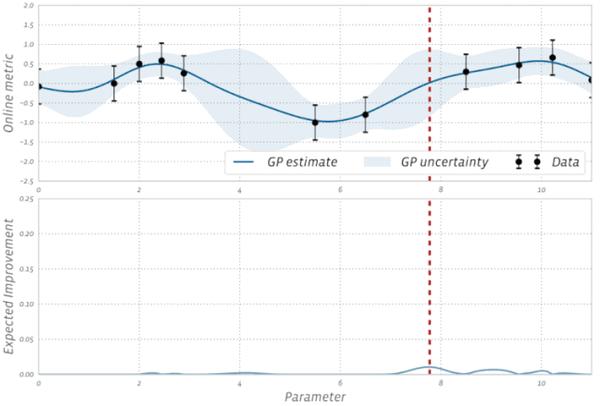
由于 f(x) 是一个乱数变量，I(x) 同样也为乱数变量，但是 f(x) 的后验是从高斯过程数学模型中分析得出的。基于期望改良（EI）的采集函数会选择模块点 x 以最大化 I(x) 的期望值，这一过程会基于高斯过程后验。EI 是一种流行的采集函数，因为此种期望具有易计算的分析形式，且在实践中也有非常好的表现。右图展示了上述数学模型的 EI：

最大化 EI（红色虚线）的模块在下一个试验中会展开试验。数学模型随后用该试验的结论展开更新，并重新计算 EI 以选择新的候选模块。这一循环会持续到搜寻结束，上图展示了几次迭代的结论。

高斯过程假设响应表面是平滑的，这将允许我们参考模块内部空间的近邻观察值，从而确定可能将的下一组模块是怎么样的。高斯过程使我们相信已经彻底探索了内部空间，因而不需要如分层搜寻那样实际试验每一可能将的模块值。

将可计算性强化应用到新浪网试验

可计算性强化方式应用作修正新浪网控制系统时需要面对几项挑战，在 Facebook 的学术论文中对此展开了描述。

约束：除了需要强化的指标，还有要要满足的约束。那些约束一般来说本身是带噪声的指标，因而我们要考虑它们的可行的后验分布。

批量试验：由于新浪网试验相当耗时间，它们一般来说不是按线性序列运转，如上动图所示，它们是以大批量在并行试验中运转。在我们的试验中，我们每次频繁地评估 50 个配置，因而需要能返回大批量可评估点的可计算性强化过程。

EI 拥有能解决那些问题的扩展，然而当噪声等级达到 A/B 试验的众所周知等级时，采用启发式方式处理噪声的结论很糟糕。由于观察结论中的噪声，不仅对 f(x) 值存有不确定，而且对哪个 x*和 f(x*) 是目前最佳的观察结论也存有不确定。处理观察结论噪声的常用方式是忽略它，并通过插件式的估计器替换 f(x*) 的高斯过程均值估计。

在学术论文中，Facebook 描述了一种可计算性方式来处理观察噪声，其中包括了 EI 期望值噪声引入的后验不确定性。即，我们在 f(x) 和 f(x*) 的联手后验下计算 I(x) 的期望值，而不是在 f(x) 的后验下计算它。这个期望值不再拥有相近 EI 的形式，然而我们能轻易地从 GP 后验中采样过去观察 f(x_1), …, f(x_n) 的值，并且条件分布 f(x) | f(x_1), …, f(x_n) 有相近的形式。因而该期望值服从蒙特卡罗近似，其中我们采样 f(x_1), …, f(x_n) 然后以相近的形式求条件期望 E[I(x) | f(x_1), …, f(x_n)]。学术论文中展示了拟蒙特卡罗方式（quasi-Monte Carlo）的结合怎样为该期望提供更多了很好的估计，并能高效地对其展开强化。

Facebook 利用可计算性强化得到的结论

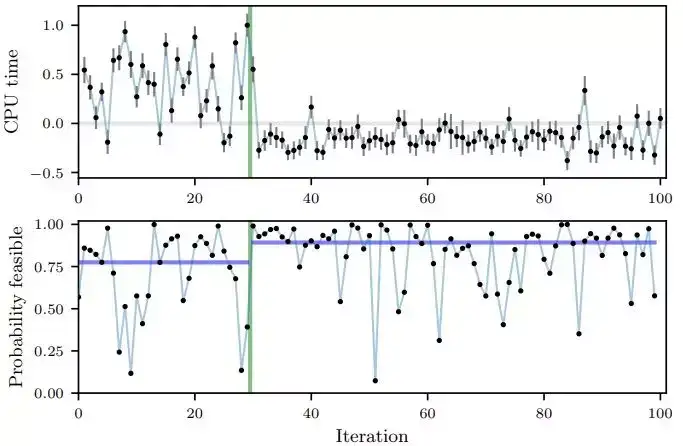
研究者采用学术论文中描述的方式来强化 Facebook 中的数个控制系统，并在学术论文中描述了两种强化案例。第一个案例是强化 Facebook 一个排序控制系统的 6 个模块。那些特定模块和索引器相关，该索引器聚集了要被发送到预测数学模型的内容。第二个案例是为 HHVM 强化 7 个数值C++ flag。强化的目标是减少网页伺服器的 CPU 占用，并满足不增加峰值内存占用的约束。下面这张来自学术论文中的图展示了每一试验配置的 CPU 占用（总共 100 个配置）随迭代次数的变化，以及每一点满足内存约束的概率。