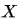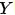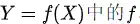概要
依照机器自学的各项任务或应用领域情况的相同,我们一般来说把机器自学分成五类:
1、监督管理自学(Supervised Learning,SL),这类演算法的组织工作基本原理是采用带条码的体能训练统计数据来自学输入表达式
转化成为输入表达式
的初等变换,换言之就是解方程组
。更进一步地,监督管理自学又可行业龙头为如下表所示四类:
重回(Regression):预估两个值,如预估雨量、楼价等,较此基础的演算法有:Linear Regression进行分类(Classification):预估两个条码,如预估“患病”或“身心健康”,相片上是何种鸟类等,较此基础的演算法有:Logistic Regression、Naive Bayes、K-Nearest Neighbors(KNN)【另】:软件系统(Ensembling)也能进行分类为监督管理自学的一类,它将数个原则上偏弱的机器自学数学模型的预估紧密结合起来,以造成更精确的预估,较此基础的演算法有Bagging with Random Forests、Boosting with XGBoost
2、非监督管理自学(Unsupervised Learning,UL),这类演算法的组织工作基本原理从无条码的体能训练统计数据中自学统计数据的下层内部结构。更进一步地,非监督管理学习又可行业龙头为如下表所示四类:
关连(Association):辨认出子集中工程项目与此同时出现的机率,如透过预测大型超市BIGBANG10,辨认出咖啡常常和换尿布一同买回(咖啡与换尿布的故事情节),较此基础的演算法有:Apriori控制点(Clustering):对统计数据进行各组,以期第四组第一类比组间第一类更相近,较此基础的演算法有:K-Means最优化(Dimensionality Reduction):增加统计数据集的表达式数目,与此同时确保关键的关键信息不被遗失。降维能透过求逆方式和RosettaDock方式来与此同时实现,求逆是继续执行从高维流形到低维流形的切换,RosettaDock是优先选择原初表达式的开集,较此基础的演算法有:PCA3、加强自学(Reinforcement Learning,DL),让agent依照当前环境状态,透过自学能够获得最大回报的行为来决定下一步的最佳行为。
与此同时实现
以上列出的演算法都是简单常见的,基于scikit-learn能仅用几行代码就完成数学模型体能训练、预估、评估和可视化。关于演算法的基本原理知乎上有很多精彩的回答,这里不会赘述,仅给出代码的与此同时实现与可视化。
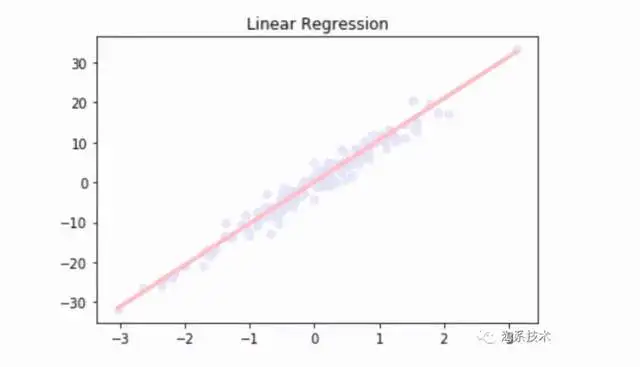
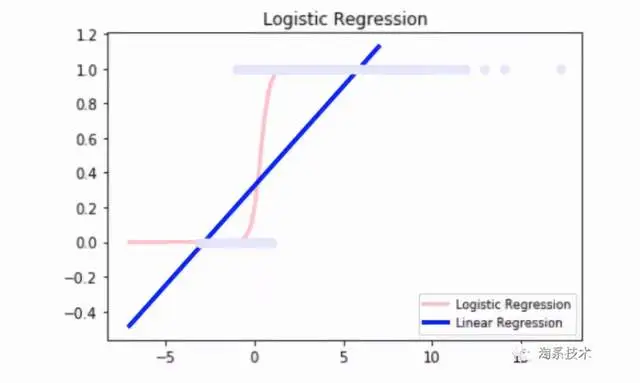
Linear Regression
它为表达式分配最佳权重,以创建一条直线或两个平面或更高维的超平面,使得预估值和真实值之间的误差最小化。具体基本原理参考:用人话讲明白线性重回LinearRegression – 化简可得的文章 – 知乎。下面以一元线性重回为例,给出代码与此同时实现。
Logistic Regression
虽然写着回归,但实际上是一类二进行分类演算法。它将统计数据拟合到logit函数中,所以称为logit重回。简单来说就是基于一组给定的表达式,用logistic function来预估这个事件的机率,给出两个介于0和1之间的输入。具体基本原理参考:用人话讲明白逻辑重回Logistic regression – 化简可得的文章 – 知乎,下面给出代码的与此同时实现。
Naive Bayes
朴素贝叶斯是一类基于贝叶斯定理的进行分类方式,它会假设两个类中的某个特征与其他特征无关。这个数学模型不仅非常简单,而且比许多高度复杂的进行分类方式表现得更好。具体基本原理参考:朴素贝叶斯演算法基本原理小结 – 刘建平Pinard,下面给出代码的与此同时实现。
K-Nearest Neighbors
这是用于进行分类和重回的机器自学演算法(主要用于进行分类)。它考虑了相同的质心,并采用欧几里得函数来比较距离。接着预测结果并将每个点进行分类到组中,以优化它,使其与所有最接近的点一同放置。它采用k个最近邻的多数票对统计数据进行进行分类预估。具体原来参考:K近邻法(KNN)基本原理小结 – 刘建平Pinard,下面给出代码的与此同时实现。
Decision Tree
遍历树,并将关键特征与确定的条件语句进行比较。它是降到左边的子分支还是降到右边的子分支取决于结果。一般来说,更关键的特性更接近根,它能处理离散表达式和连续表达式。具体基本原理参考:深入浅出理解决策树演算法(一)-核心思想 – 忆臻的文章 – 知乎,下面给出代码的实现。
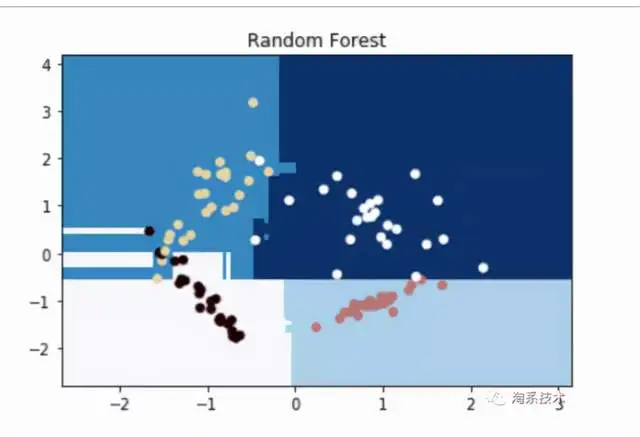
Random Forest
随机森林是决策树的子集。随机采样统计数据点构造树、随机采样特征开集分割,每棵树提供两个进行分类。得票最多的进行分类在森林中获胜,为统计数据点的最终进行分类。具体原来参考:独家 | 一文读懂随机森林的解释和与此同时实现 – 清华大学统计数据科学研究院的文章 – 知乎,下面给出代码的与此同时实现。
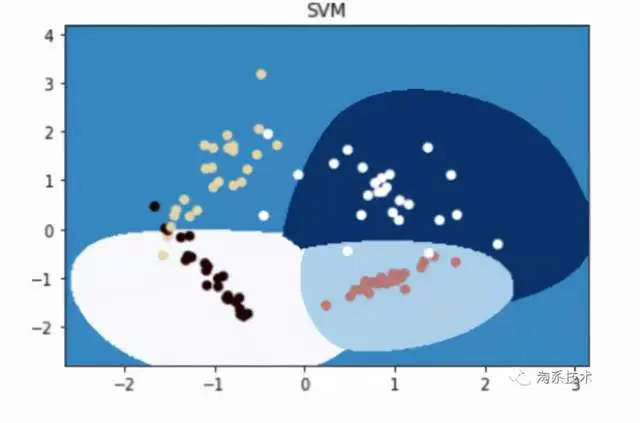
Support Vector Machines
它将统计数据映射为空间中的点,使得相同类别的点能被尽可能宽的间隔分隔开,对于待预估类别的统计数据,先将其映射至同一空间,并依照它落在间隔的哪一侧来得到对应的类别。具体原来参考:看了这篇文章你还不懂SVM你就来打我 – SMON的文章 – 知乎,下面给出代码与此同时实现。
import matplotlib.pyplot as pltimport numpy as npfrom sklearn.model_selection import train_test_splitfrom sklearn.datasets import make_classification
# SVMfrom sklearn import svm# 1. 准备统计数据svm_X_train, svm_y_train = make_classification(n_features=2, n_redundant=0, n_informative=2, random_state=1, n_clusters_per_class=1, n_classes=4)# 2. 构造体能训练与测试集l, r = svm_X_train[:, 0].min() – 1, svm_X_train[:, 0].max() + 1b, t = svm_X_train[:, 1].min() – 1,svm_X_train[:, 1].max() + 1n = 1000grid_x, grid_y = np.meshgrid(np.linspace(l, r, n), np.linspace(b, t, n))svm_X_test = np.column_stack((grid_x.ravel(), grid_y.ravel()))# 3. 体能训练数学模型# svm_model = RandomForestClassifier(max_depth=4)svm_model = svm.SVC(kernel=rbf, gamma=1, C=0.0001).fit(svm_X_train, svm_y_train)svm_model.fit(svm_X_train, svm_y_train)# 4. 预估统计数据svm_y_pred = svm_model.predict(svm_X_test)# 5. 可视化grid_z = svm_y_pred.reshape(grid_x.shape)plt.figure(SVM)plt.title(SVM)plt.pcolormesh(grid_x, grid_y, grid_z, cmap=Blues)plt.scatter(svm_X_train[:, 0], svm_X_train[:, 1], s=30, c=svm_y_train, cmap=pink)plt.show()
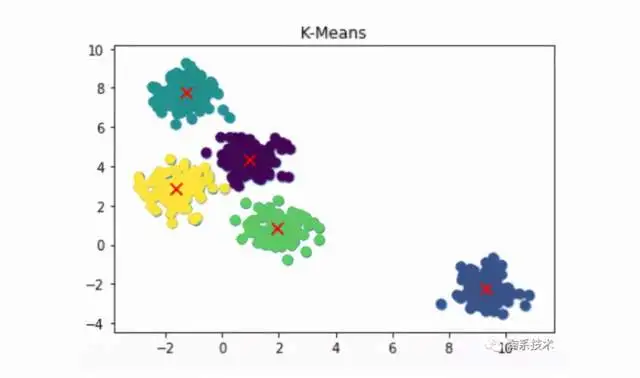
K-Means
将统计数据划分到K个控制点簇中,使得每个统计数据点都属于离它最近的均值(即聚类中心,centroid)对应的集控制点簇。最终,具有较高相近度的统计数据第一类划分至同一类簇,将具有较高相异度的统计数据第一类划分至相同类簇。具体基本原理参考:用人话讲明白快速控制点kmeans – 化简可得的文章 – 知乎,下面给出代码的与此同时实现。
import matplotlib.pyplot as pltimport numpy as npfrom sklearn.model_selection import train_test_splitfrom sklearn.datasets.samples_generator import make_blobs
# K-means 各项任务为控制点 n_classes=5from sklearn.cluster import KMeans
# 1. 准备统计数据kmeans_X_data, kmeans_y_data = make_blobs(n_samples=500, centers=5, cluster_std=0.60, random_state=0)# 2. 体能训练数学模型kmeans_model = KMeans(n_clusters=5)kmeans_model.fit(kmeans_X_data)# 3. 预估数学模型kmeans_y_pred = kmeans_model.predict(kmeans_X_data)# 4. 可视化plt.figure(K-Means)plt.title(K-Means)plt.scatter(kmeans_X_data[:,0], kmeans_X_data[:, 1], s=50)plt.scatter(kmeans_X_data[:, 0], kmeans_X_data[:, 1], c=kmeans_y_pred, s=50, cmap=viridis)centers = kmeans_model.cluster_centers_plt.scatter(centers[:,0], centers[:, 1], c=red, s=80, marker=x)plt.show()
PCA
一类常见的最优化技术,顾名思义,PCA帮助我们找出统计数据的主要成分,主成分基本上是线性不相关的向量,用选出的k个主成分来表示统计数据,来达到最优化的目的。具体基本原理参考:如何通俗易懂地讲解什么是 PCA 主成分预测?- 马同学的回答 – 知乎,下面给出代码与此同时实现。
import matplotlib.pyplot as pltimport numpy as npfrom sklearn.model_selection import train_test_splitfrom sklearn.datasets import make_classification
# PCAfrom sklearn.decomposition import PCAfrom sklearn.datasets import load_iris
# 1. 准备统计数据pca_data=load_iris()pca_X_data=pca_data.datapca_y_data=pca_data.target# 2. 体能训练数学模型, 维度为2pca_model=PCA(n_components=2) # 3. 最优化reduced_X=pca_model.fit_transform(pca_X_data)# 4. 可视化red_x,red_y=[],[]blue_x,blue_y=[],[]green_x,green_y=[],[]
for i in range(len(reduced_X)): if pca_y_data[i] ==0: red_x.append(reduced_X[i][0]) red_y.append(reduced_X[i][1]) elif pca_y_data[i]==1: blue_x.append(reduced_X[i][0]) blue_y.append(reduced_X[i][1]) else: green_x.append(reduced_X[i][0]) green_y.append(reduced_X[i][1])
plt.figure(PCA)plt.title(PCA)plt.scatter(red_x,red_y,c=r)plt.scatter(blue_x,blue_y,c=b)plt.scatter(green_x,green_y,c=g)plt.show()
总结
经验的好途径。
原文链接
本文为阿里云原创内容,未经允许不得转载。