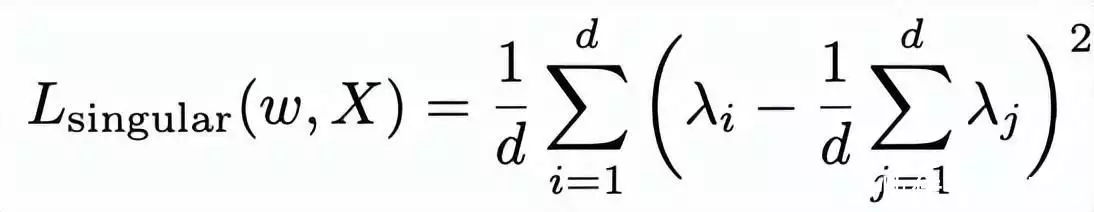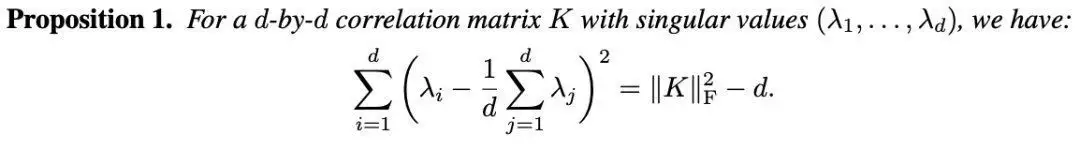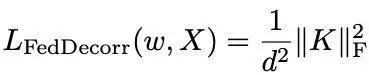施宇钧NUS 征稿
随著广度自学大获获得成功,为保护使用者统计数据个人隐私显得愈来愈关键。
联邦政府自学(Federated Learning)不断涌现,这是一类如前所述个人隐私为保护的原产式系统机器自学框架。
它能让原始统计数据留存在邻近地区,让多番联手共享资源数学模型体能训练。
但它有两个难题——统计数据的同质化(data heterogeneity),即相同的合作方的邻近地区统计数据源自相同的原产,这将严重负面影响自上而下数学模型的最后操控性,另一面其原因也非常复杂。
二进制颤动、香港科技大学及中国科学院自动化所的科学研究者们首度辨认出了关键性负面影响不利因素。
即:统计数据同质化引致了表观的层次塌缩(dimensional collapse),继而大幅管制了数学模型的理解能力,负面影响了最后自上而下数学模型的操控性。
为的是减轻而此难题,科学研究相关人员明确提出了两个新联邦政府自学二阶项:FedDecorr。
结果表明,使用该方法后,统计数据同质化带来的层次塌缩难题被有效减轻,显著提升数学模型在该场景下的操控性。
同时而此方法实现简单,基本上不会带来额外计算负担,能很容易地加入到多种联邦政府自学算法上。
如何负面影响?
观察一:更严重的统计数据同质化会为自上而下数学模型(global model)带来更严重的层次塌缩
首先,为的是更好地理解数据同质化是如何负面影响自上而下数学模型输出表观的,科学研究相关人员探索了随著统计数据同质化愈来愈严重,自上而下数学模型输出表观是如何而变化的。
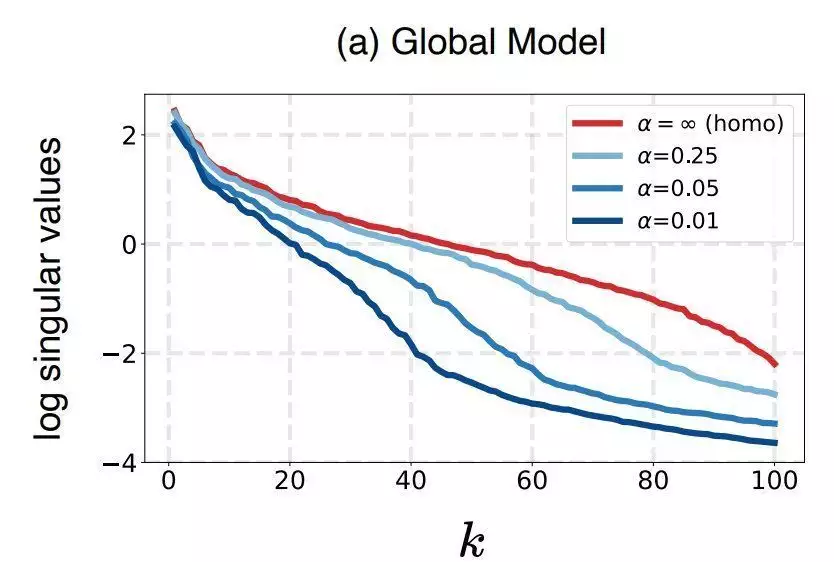
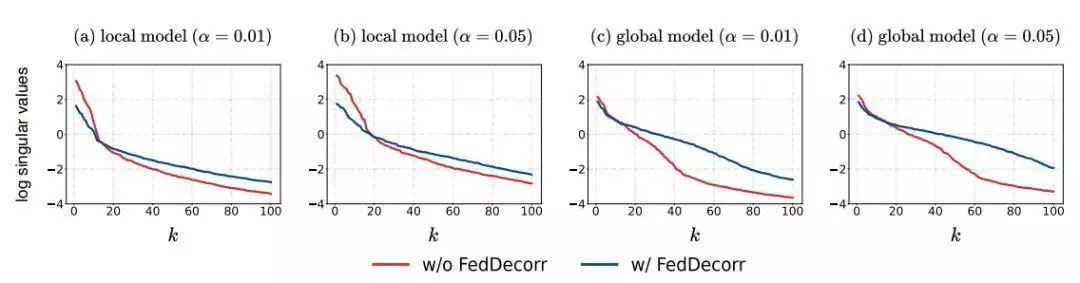
如前所述数学模型输出的表观,估计其表观原产的协方差矩阵(covariance matrix),并且按照从大到小的顺序可视化了该协方差矩阵的特征值。结果如下图所示。α越小,同质化程度越高,α为正无穷时为同质化场景。k为特征值的index。
对于该曲线,如果特征值大部分相对较大,即意味着表观能够更加均匀地原产在相同的特征方向上。而如果该曲线只有前面少数特征值较大,而后面大部分特征值都很小,就意味着表观原产被压缩在少数特征方向上,即层次塌缩现象。
因此,从图中能看到,随著统计数据同质化程度愈来愈高(α越来越小),层次塌缩的现象就愈来愈严重。
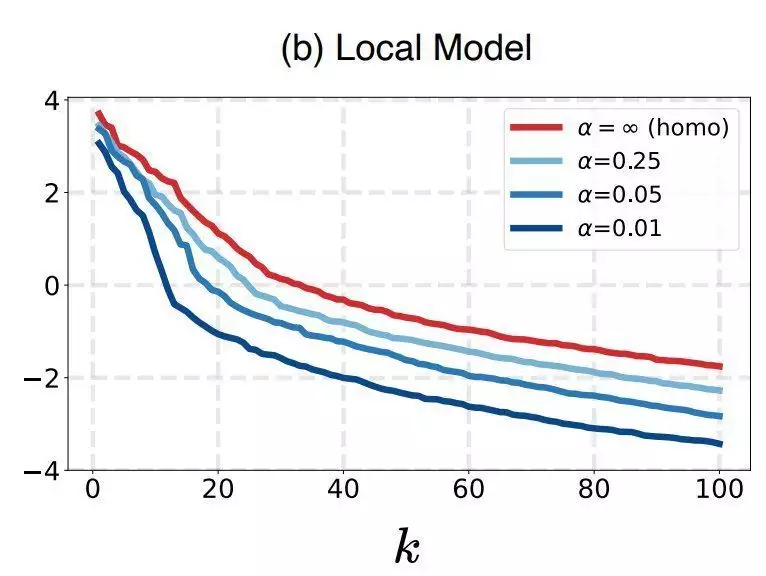
观察二:自上而下数学模型的层次塌缩源自联邦政府参与各方的局部数学模型的层次塌缩
部数学模型的层次塌缩。
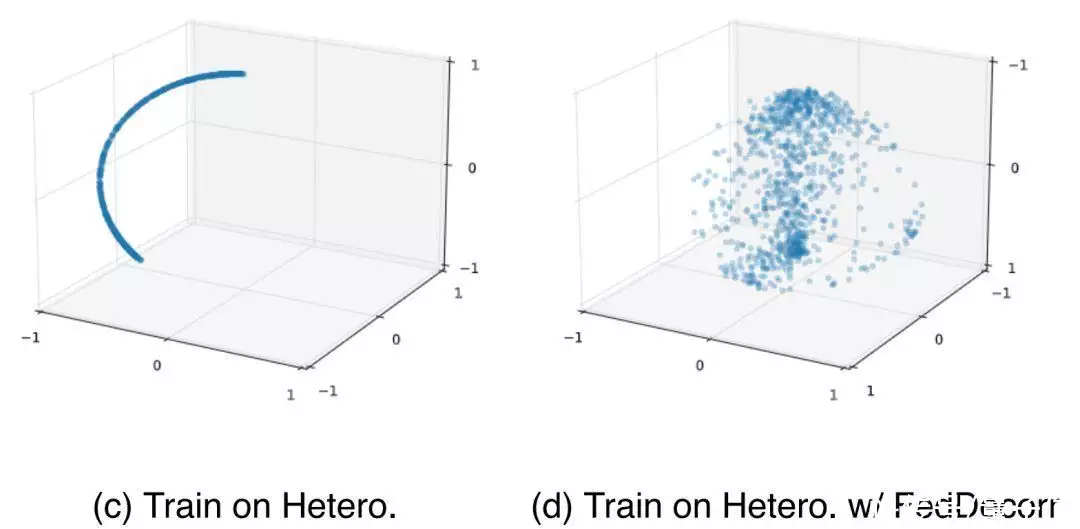
为的是进一步验证该推断,作者使用与观察1类似的方法,针对相同程度统计数据同质化场景下得到的局部数学模型进行了可视化。结果如下图所示。
从图中能看到,对于局部数学模型,随著统计数据同质化程度的提升,层次塌缩的现象也愈来愈严重。因此得出结论,。
怎么解决?
体能训练阶段来解决联邦政府自学中的表观层次塌缩难题。
首先,两个最直观的可用的二阶项为以下形式:
其中
为第
个特征值。该二阶项将约束特征值之间的方差变小,从而使得较小的特征值不会偏向于0,继而减轻层次塌缩。
然而,直接计算特征值往往会带来数值不稳定,计算时间较长等难题。因此借助以下proposition来改进方法。
为的是方便处理,需要对表观向量做z-score归一化。这将使得协方差矩阵变成相关系数矩阵(对角线元素都是1)。
如前所述这个背景,能得到以下proposition:
而此proposition意味着,原本较为复杂的如前所述特征值的二阶化项,能被转化为以下易于实现且计算方便的目标:
该二阶项即是简单的约束表观的相关系数矩阵的Frobenius norm更小。科学研究相关人员将该方法命名为FedDecorr。
因此,对于每个联邦政府自学合作方,邻近地区的优化目标为:
其中
为分类的交叉熵损失函数,β为两个超参数,即FedDecorr二阶项的系数。
实验结果
首先,验证使用FedDecorr是否能有效减轻层次塌缩。
在α=0.01/0.05这两个强统计数据同质化的场景下,观察使用FedDecorr对数学模型输出表观的负面影响。
结果如下图所示。
能看到,使用FedDecorr能有效地减轻邻近地区局部数学模型的层次塌缩,从而进一步减轻自上而下数学模型的层次塌缩。
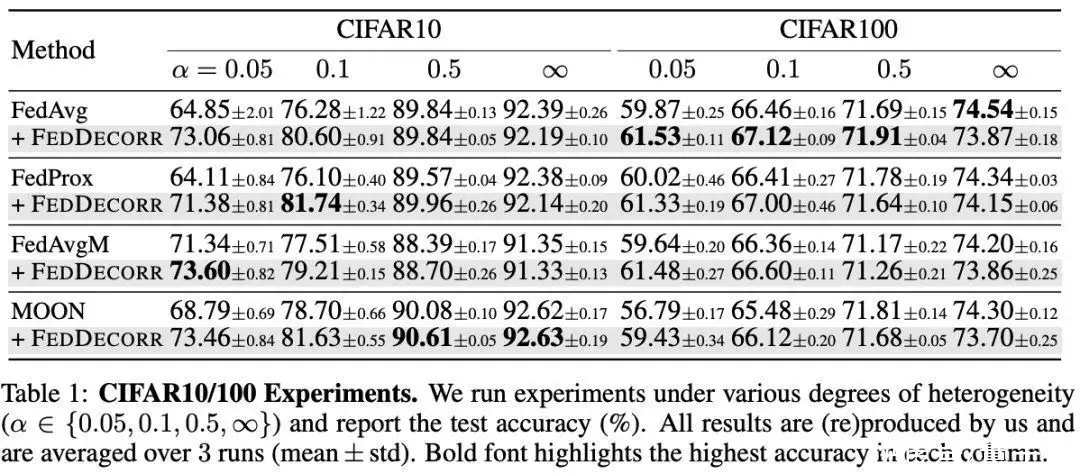
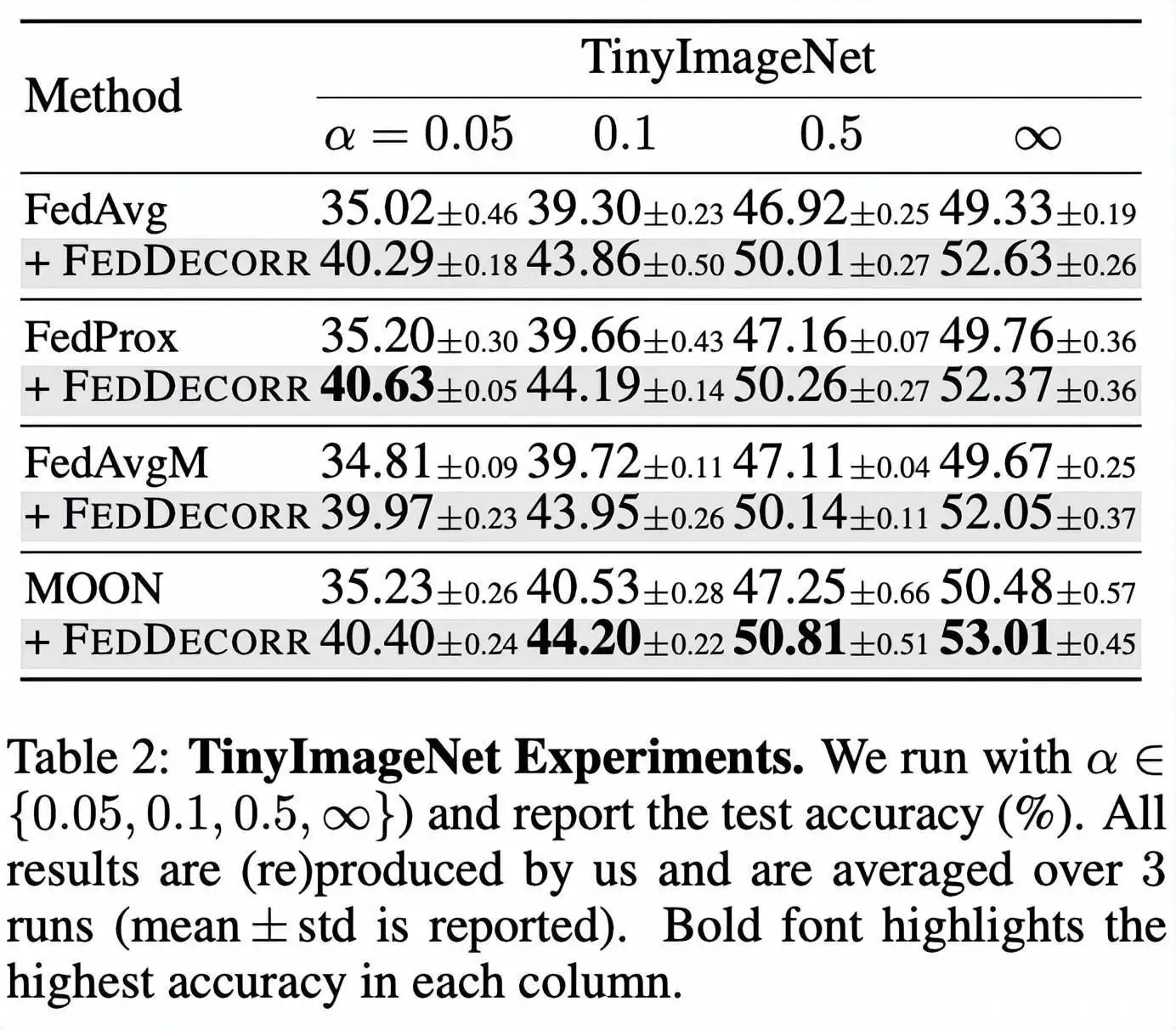
在CIFAR10/100两个统计数据集上验证方法。科学研究团队辨认出FedDecorr能很方便的加入到之前提出的多个联邦政府自学方法,并且带来显著提升:
同时,为的是展示方法的可扩展性,作者在较大规模统计数据集(TinyImageNet)上进行了实验,并且也观察到了显著提升:
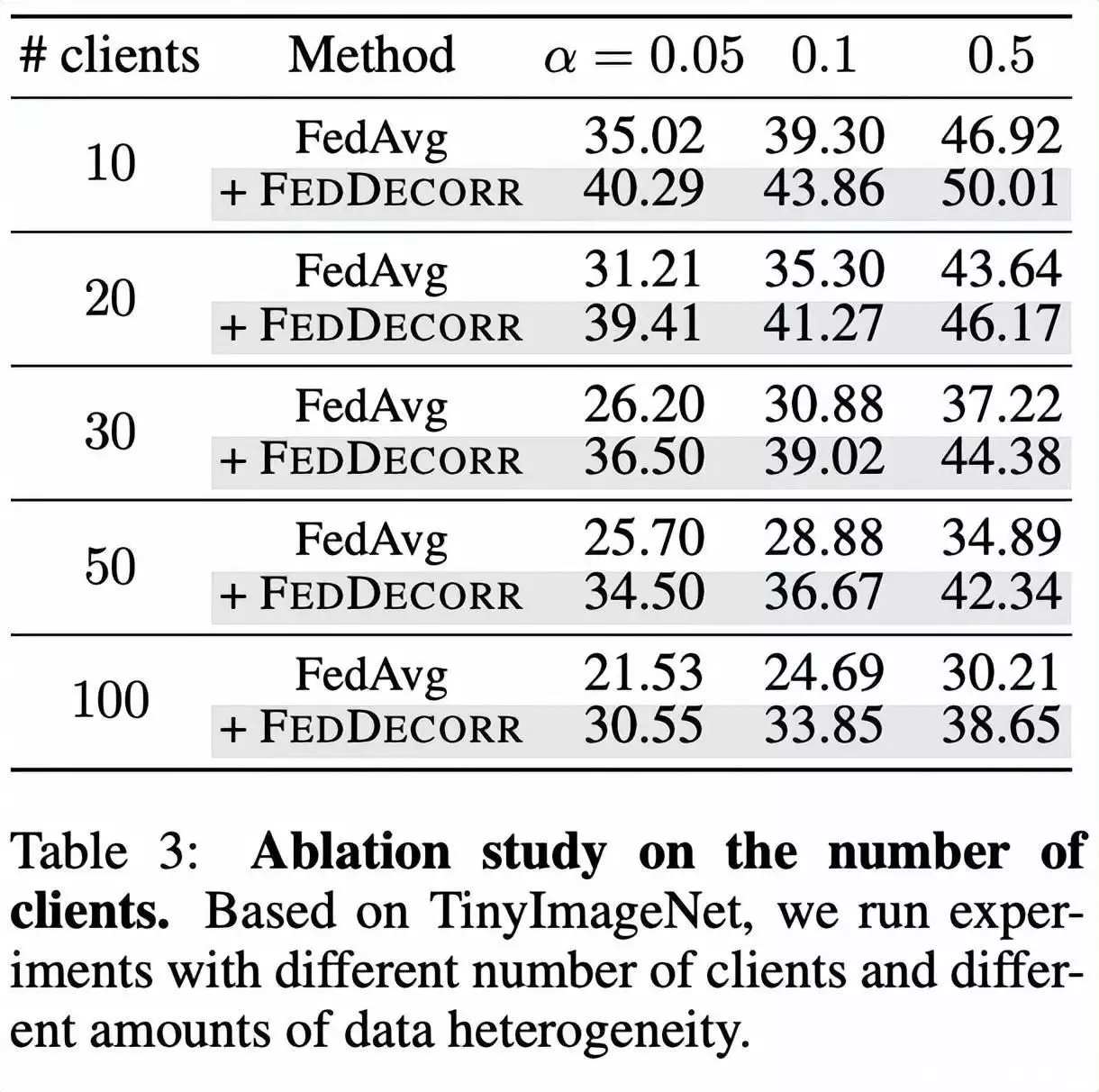
此外还如前所述TinyImageNet,验证了FedDecorr在更大规模联邦政府合作方的场景下的有效性。
结果如下表。通过实验结果展示了FedDecorr能被用于较大规模联邦政府合作方的场景。
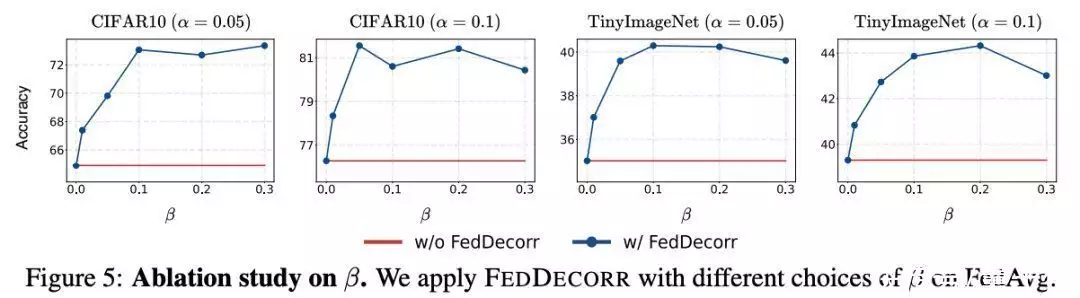
FedDecorr对二阶项系数(超参数β)的鲁棒性结果如下图所示。
通过实验,辨认出FedDecorr对于其超参数β有较强的鲁棒性。
同时辨认出将β设为0.1是两个不错的默认值。
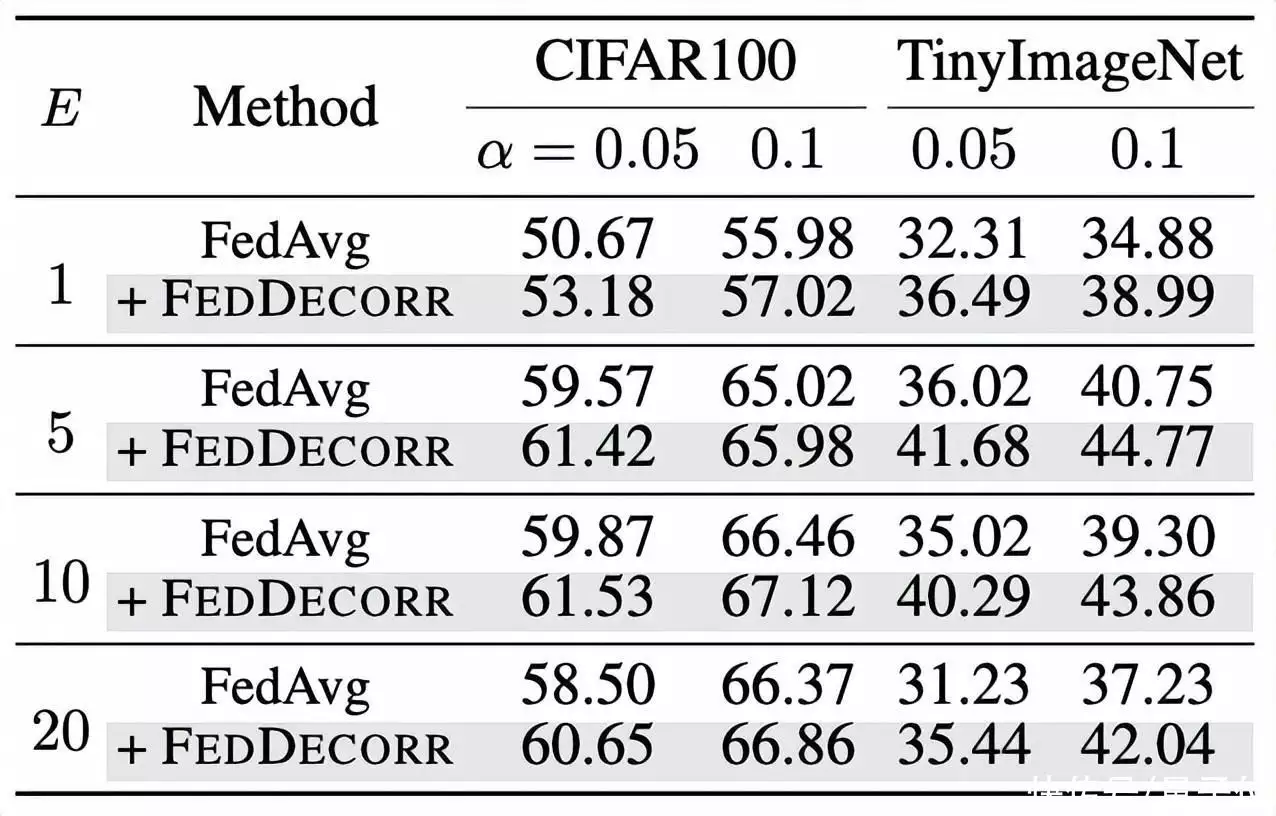
最后,科学研究相关人员验证了在联邦政府自学时,使用相同的local epoch下FedDecorr也能带来普遍的提升:
论文地址:
https://arxiv.org/abs/2210.00226代码链接:https://github.com/bytedance/FedDecorr— 完 —
量子位 QbitAI · 头条号签约