中国剩余定理的几何意义

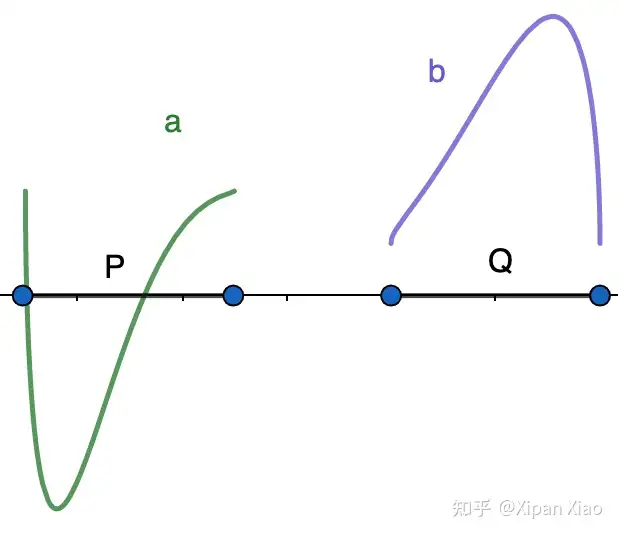
他们先看两个单纯的一元表达式的范例：假如三个闭开集不平行，则能表述两个自上而下已连续表达式，使在开集下面等同于科水狼的表达式值。更具体内容地，考量极线 $R$ \mathbb{R} 上的三个不平行的闭区间 $P\capQ=\emptyset$ P\cap Q =\emptyset 。设 $a,b$ a, b 是 $R$ \mathbb{R} 上的三个已连续（扁平）表达式，所以他们能内部结构两个已连续（扁平）表达式 $f$ f ，使它在三个闭区间上的管制分别为 $a,b$ a, b 。

表述在不平行子集上的三个扁平表达式

这事儿是显然的（比如他们只要把下面两段图像首尾用直线段连接起来，就得到两个满足条件的自上而下已连续表达式图像）。这是因为闭区间 $P,Q$ P,Q不平行，所以他们能自由的指定在各自区间上的表达式值。一般地，（使用“单位分解”之类的技术），能找到两个扁平表达式 $u$ u ，它在 $P$ P 上恒为 $1$ 1 ，在 $Q$ Q 上恒为零；类似的找到 $v$ v 在 $Q$ Q 上恒为 $1$ 1 ，在 $P$ P 上恒为零：

单位分解

然后令 $f=au+bv$ f=au+bv即可，它显然满足条件，且是已连续（扁平）的。它的值在开集 $P\cupQ$ P\cup Q 上是确定的。

这事儿跟我国余下不等式有啥关系呢？他们先看数论里边的余下不等式。为叙述单纯，他们只考量三个素数的情况：假如整数 $p,q$ p, q互素，也就是 $(p,q)=1$ (p, q)=1 ，则同余方程组

$x\equiva(modp)x\equivb(modq)$ \begin{align*} x &\equiv a \pmod p\\ x &\equiv b \pmod q\\ \end{align*} ，

在模 $pq$ pq 的余下系中有唯一解。它的证明也很单纯。首先能选取整数 $u$ u 满足

$u\equiv1(modp)u\equiv0(modq)$ \begin{align*} u &\equiv 1 \pmod p\\ u &\equiv 0 \pmod q\\ \end{align*} ，

这是因为 $p,q$ p, q 互素，从而有 $y,z$ y,z 使Bezout等式成立 $py+qz=1$ p y + q z = 1，令 $u=qz$ u=qz 即可。类似的选取整数 $v$ v 满足

$v\equiv0(modp)v\equiv1(modq)$ \begin{align*} v &\equiv 0 \pmod p\\ v &\equiv 1 \pmod q\\ \end{align*} ，

再令 $x=au+bv$ x = a u + b v 即可。

能看出类似的地方：区间不平行 $P\capQ=\emptyset$ P\cap Q=\emptyset 对应整数互素 $(p,q)=1$ (p, q)=1，这是“单位分解”（对应Bezout等式）存在的前提。而单位分解和内部结构解的过程一模一样。其实它们都是环上余下不等式的特例。在一般交换环中，余下不等式的叙述类似：假如交换环 $A$ A 的理想 $p,q$ p, q 互素，也就是 $(p,q)=(1)$ (p, q)=(1) ，则上述同余方程组在模 $p\capq$ p\cap q 的余下系中有唯一解。

注意到 $R$ \mathbb{R} 上的已连续（扁平）实值表达式全体构成两个交换环 $A=Γ(R)$ A=\Gamma(\mathbb{R}) ，加法和乘法就是表达式逐点相加相乘。现在令 $p,q$ p, q 是在闭区间 $P,Q$ P,Q 上为零的表达式全体：

$p={f\inA∣fP\equiv0}q={f\inA∣fQ\equiv0}$ \begin{align*} p &=\{f\in A\mid f_P\equiv 0\}\\ q &=\{f\in A\mid f_Q\equiv 0\} \end{align*} ，

则容易验证 $p,q$ p, q 是 $A$ A 的理想。他们用符号 $p=I(P),q=I(Q)$ p=I(P), q=I(Q) 表示，所以 $p\capq=I(P\cupQ)$ p\cap q=I(P\cup Q) 表示在三个开集上都为零的表达式。而且这俩理想是互素的：下面的单位分解满足 $u\inq,v\inp$ u\in q, v\in p ，且 $u+v\equiv1$ u+v\equiv 1 为常数表达式 $1$ 1 ，这说明 $p+q=(p,q)=(1)$ p+q=(p, q) = (1) 。然后，环上的余下不等式就断言：下述同余方程组，在模 $p\capq$ p \cap q 的余下系中存在唯一解

$f\equiva(modp)f\equivb(modq)$ \begin{align*} f\equiv a \pmod p\\ f\equiv b \pmod q \end{align*} 。

注意到 $f\equiva(modp)$ f \equiv a \pmod p 就是说 $f-a\inp$ f-a\in p 。也就是 $f-a$ f-a 在 $P$ P 上取零值，或者说 $f$ f 在 $P$ P 上的管制等同于 $a$ a 。所以这就回到了他们最开始的范例。

更进一步，假如 $P,Q$ P, Q 三个都是单点集，且只考量多项式表达式，就得到了拉格朗日插值不等式。此时单点集对应了环中的极大理想，而三个极大理想之间自然是互素的。

这里其实也给出了理想的欧几里得象征意义：表达式环的理想对应着空间的闭开集；（素理想对应着不可约的闭开集）极大理想对应着单点集；理想互素对应着闭开集不平行；三个单点集当然不平行，对应着极大理想之间当然互素；表达式包含于理想，对应着表达式在闭开集上取值为零；理想的包含对应闭开集的（反向）包含；理想的交对应闭开集的并……这些对应是代数欧几里得最基本的思想：欧几里得陈述能一对一地翻译成代数陈述，反之亦然。

这里他们要求 $P,Q$ P, Q都是闭的，因为已连续表达式的零点集是闭的。而理想对应的开集，是它里边所有表达式的零点集的交（所以理想越大，地盘越小，这真是悲哀[doge]），而闭集的任意交依然是闭的。