Vector autoregressive model 是多元化天数字符串预测中最此基础的同族微积分模型众所周知,他们能从三个视角来认知它,
从纵向较为上看,它是单抒发式天数字符串Autoregressive(AR)微积分模型在多元化天数字符串上的派生;
从纵向较为上看,它和它的其它爸爸妈妈VMA,VARMA等都是在用差值刻划两个相对平稳的控制系统;
上面他们主要就阐释 VAR的物理性质,内生性抒发式与斑籽抒发式,VAR的应用领域(吓人在这儿)
1)VAR的物理性质
矢量自重回微积分模型的微积分抒发如下表所示,Zt是多元化抒发式在t关键时刻的值域,透过天数推移微分能将矢量自重回的操作过程紧凑型的唱出;
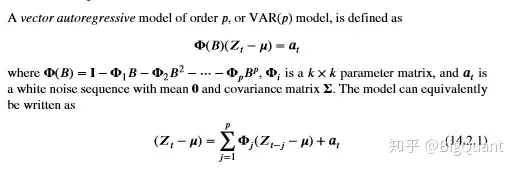
就像他们能轻而易举的从单抒发式重回迈向多抒发式重回,从AR操作过程迈向VAR操作过程的微积分推导也是类似于的;
他们在做Bayesian的这时候也须要加进 Yule-walker 方程组:
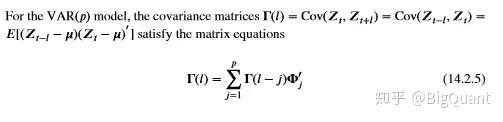
总之,最轻二乘也是能的,因此当微积分模型不相对平稳时最轻二加法估算出的模块还能维持连续性;
2) 内生性抒发式与斑籽抒发式
内生性抒发式就是参与微积分模型并由微积分模型体系内决定的抒发式,斑籽抒发式时由微积分模型外的因素决定的抒发式,他们举两个例子便于认知:
下图是两个VARMA微积分模型的部分抒发形式,公式本身经过了变换不易于认知,但是他们从图中能看到Z2是由Z1决定而Z1仅仅由a(随机扰动决定),那么在这个方程组组里,Z1是斑籽的,Z2是内生性的;

VAR微积分模型本身,从微积分视角上来说并没有强制要求所有的抒发式均为内生性抒发式,例子如下表所示:

在上图的 VAR(1) model里,完全能强制要求Z2仅仅由Z1决定,而第两个方程组中的第二个系数为0,也就是说其中两个抒发式是完全独立的AR操作过程,而另两个抒发式受它的影响。python,R等等很多函数都提供了斑籽抒发式的接口,如下表所示图:

你能选择一部分抒发式作为exog,其实质是在进行Bayesian前早已经将那一部分模块设置为0;
总之,在大部分日常微积分模型中,既然用VAR,就假定是两个相互影响的关系,都是内生性或者用微积分模型估算模块时没有绝对的0出现也是很正常的。
3)VAR 的应用领域
多元化天数字符串预测在现实中有很多应用领域,比如经济,商业,社会科学,地球物理,环境科学,工程学等等;
比如,他们可能须要研究压力,温度之间随着天数的动态关系;如下表所示图:
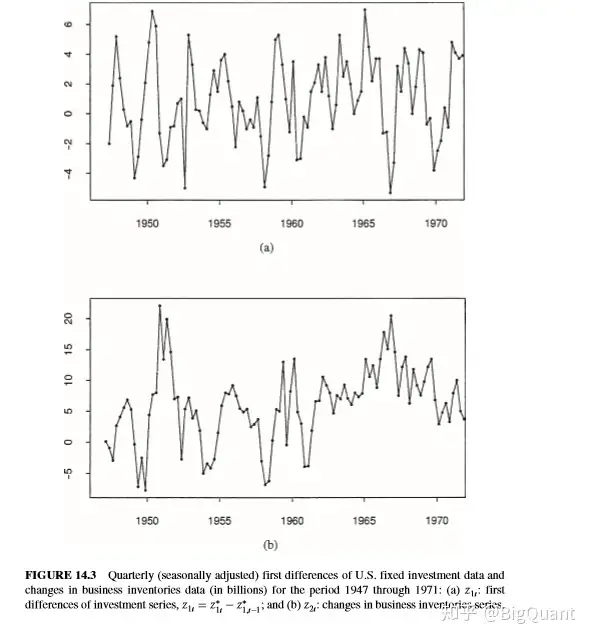
但凡涉及到多元化天数字符串预测,第两个就想到VAR和它的变体们,有如下表所示几点原因:
第一,在相对平稳的条件下,VAR微积分模型的Bayesian与最轻二乘估算是一致的,因此有许许多多统计上的优良物理性质,便于区间估算,误差预测和微积分模型诊断等;
第二,VAR能刻划抒发式之间相互影响的动态线性相关关系,不论是用在预测,解释还是敏感性预测都明确的方式;
前往平台进一步了解相关内容:











