授人以鱼比不上少击众,这首诗会如是说怎样通过“语言学检验”来对照机器学习演算法操控性。掌控了这个方式后,他们就不须要再Auterive,而能自己预测演算法操控性。
具体而言推论如下表所示,在对照三个演算法在数个统计数据K568的整体表现时:
假如样品张佩佩(paired)且合乎概率密度函数,优先选择采用张佩佩t检验(paired t test)。假如样品不合乎概率密度函数,但合乎张佩佩,采用Wilcoxon Signed Ranks test。假如样品既不合乎概率密度函数,也不合乎张佩佩,甚至样品量都不那样大,能试著Mann Whitney U test。更为重要的是,MW是用以处置分立量测(independent measures)统计数据,要分情形探讨,后文会剖析。在对照数个演算法在数个统计数据K568的整体表现时:
假如样品合乎ANOVA(repeated measure)的假定(如正态、等国际标准差),优先选择采用ANOVA。假如样品不合乎ANOVA的假定,采用Friedman test相互配合Nemenyi test做post-hoc。假如样品量不那样,或因为某一其原因不能采用Friedman-Nemenyi,能试著Kruskal Wallis相互配合Dunns test。更为重要的是,这种方式是用以处置分立量测统计数据,要分情形探讨。该文内部结构如下表所示:(1-2) 演算法对照的其原因及圈套 (3-4) 怎样对照三个演算法 (5-6)怎样对照数个演算法 (7)怎样根据统计数据优点优先选择选择对照方法 (8)辅助工具库如是说。
1. 为何须要对照演算法操控性?
语言学家George Box说过:“All models are wrong, but some are useful”(大部份数学模型都是严重错误,或者说其中一小部分是有用的)。浅显而言,任何人演算法都有不足之处,所以不存在“通用型最优化演算法”,只有在某一情景下这种演算法可能是渐进式最优化的。
因而,评估结果演算法操控性并优先选择选择最优化演算法是十分重要的。意外的是,语言学评估结果还没有在机器学习应用领域普及化,许多评估结果常常是在两个统计数据上的单纯预测,因而断定效用十分有限。
2. 评估结果演算法中的圈套
具体而言他们常说的是要优先选择选择两个恰当的评估结果国际标准,常用的有:准确度(accuracy)、停售率(recall)、精确率(precision)、ROC、Precision-Recall Curve、F1等。
优先选择选择评估结果国际标准取决于目的和统计数据集优点。在较为平衡的统计数据K568(各类统计数据近似相等的情形下),这些评估结果国际标准操控性差别不大。而在统计数据严重倾斜的情形下,优先选择选择不适合的评估结果国际标准,如准确度,就会导致看起来很好,但实际无意义的结果。举个例子,假定某稀有血型的比例(2%),数学模型只须要预测全部样品为“非稀有血型”,那么准确度就高达98%,但毫无意义。在这种情形下,优先选择选择ROC或者精确率可能就更加适当。这方面的知识较为容易理解,许多科普书都有如是说,他们就不赘述了。
其次他们要恰当理解量测方式,常用的有
分立量测(independent measures):不同样品的观测对象是分立的,不存在关联重复量测(repeated measures):样品中采用的观测对象是相同的,仅仅是分立变量在上面的作用结果不同以及成对量测(matched pair):不同样品中采用不同的观测对象,但尽量使得样品间的观测对象成对相似举个例子,他们想要预测刷知乎时间(每天3小时 vs. 每天10小时)对于大学生成绩的影响。假如他们采用相同的20个学生,观察他们每天3小时和10小时的区别,那就是重复量测。假如他们优先选择选择40个学生,分成两组每组20人,再分别观察那就是分立量测。假如他们先找20个学生,再找20个和他们十分相似的大学生,并张佩佩观察,就是成对相似。
我们发现,当严重错误的理解量测方式时,就无法采用恰当的语言学手段进行预测。
在这首诗中他们默认:评估结果不同演算法在数个相同统计数据K568的整体表现属于重复量测,而特例将会在第七部分探讨。同时,本文如是说的方式能用于对照任何评估结果国际标准,如准确度、精确度等,本文中默认探讨准确度。
3. 两种演算法间的较为:不恰当方式
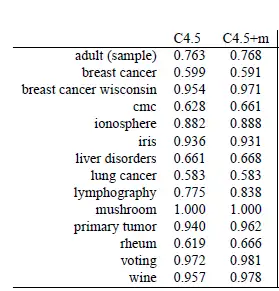
图1展示了两种决策树方式(C4.5,C4.5+m)在14个统计数据集上的准确度。那么该怎样对照两种演算法呢?先说几种严重错误(不恰当)的方式:
不恰当方式1:求每个演算法在大部份统计数据K568的均值,并较为大小。严重错误其原因:他们对于演算法在不同统计数据K568严重错误的期望不是相同的,因而求平均没有意义。换句话说,统计数据不合乎相称性(commensurate)。
不恰当方式2:进行张佩佩样品t检验(Paired t test)。显然,t test是语言学方式,能用以查看两种方式在每个统计数据上的平均差值是否不等于0。但这个方式不合适其原因有几点:
和平均那样,不同统计数据K568的严重错误不合乎相称性t-test要求样品合乎概率密度函数,显然他们无法保证不同统计数据K568的准确度合乎概率密度函数t-test对样品的大小有一定的要求,一般最低须要>30个样品。在这个例子中他们只有14个,且大部分情形下他们没有30个统计数据来做实验。因为缺乏相称性,统计结果易受到异常值影响(outliers)不恰当方式3:符号检验(sign test)是一种无参数(non-parametric)的检验,优点是对于样品分布没有要求,不要求正态性。较为方式很单纯,就是在每个统计数据K568看哪个演算法更好,之后统计每个演算法占优的统计数据集总数。以这个例子为例,C4.5在2个统计数据K568最优化,2个平手,10个最差。假如他们对这个结果计算置信区间,发现p<0.05须要至少在11个统计数据K568整体表现最优化。因而这个方式的缺点有:
符号检验是一种十分弱的检验方式,仅对照优劣损失了大量信息,失去了定量信息(quantitative),比如0.1<0.90.1<0.9 和 0.1<0.110.1<0.11的意义是那样的。正因为如此,临界值(critical value)一般都须要很大,比如这个例子中的α=0.05\alpha=0.05的临界值是11(图2)。另两个问题是,因为缺乏定量信息,许多时候很难确定“优胜”是否来自随机性。举个例子,0.99<0.991是否真的代表演算法A更好?一种看法是须要定义两个阈值,仅当差别大于阈值才能说明更好。然而这种看法的问题在于,假定演算法A在1000个统计数据K568都以“微弱优势”胜过了B,那么他们是否须要怀疑显著性?因而,根本问题还是,符号检验须要大样品量才能得出显著性。
4. 两种演算法间的较为:推荐方式
考虑到通用型性,他们须要采用非参数检验。换句话说,他们须要保证对样品的分布不做任何人假定,这样更加通用型。
方式1:Wilcoxon Signed Ranks Test(WS )是张佩佩t检验的无参数版本,同样是预测成对统计数据的差值是否等于0,或者说是通过排名(rank)而已。换个角度看,他们也能理解为符号检验的定量版本。优点如下:
无参数,不要求样品合乎概率密度函数合乎统计数据相称性,虽然是定性的(与张佩佩t检验相比)有一定的定量优点,即较大的差别对于最终结果影响更大(与符号检验相比)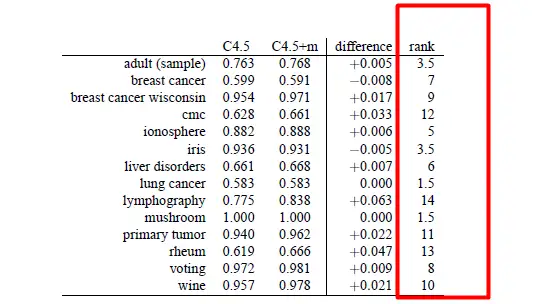
方式2(详见第七部分):Mann Whitney U test(MW)和WS那样,都是无参数的且研究排名的检验方式。MW有以下优点:
能用以检验不同的大小的样品,举例A演算法在8个统计数据K568的整体表现 vs B演算法在10个统计数据K568的整体表现。不存在张佩佩性要求,参看上一点对照的是三个样品的分布,因而不同统计数据集的严重错误应该合乎某一分布,可能不满足相称性对于量测方式的假定是:分立量测,这与他们的实际情形不符换句话说,MW是当样品量不同时才建议勉强一试,因为不合乎分立量测的假定。不同统计数据集的严重错误(准确度)不一定合乎某一分布,很可能不合乎相称性,但在某一情形下有用,详见第七部分。
总结:假如样品张佩佩且合乎概率密度函数,优先采用张佩佩t检验。假如样品不合乎概率密度函数,但合乎张佩佩,采用WS。假如样品既不合乎概率密度函数,也不合乎张佩佩,能试著MW。
5. 多种演算法间的较为:不恰当的方式
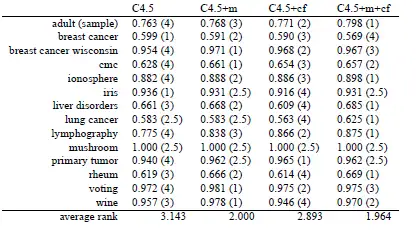
图4提供了四种演算法(C4.5,C4.5+m,C4.5+cf,C4.5+m+cf)在14个统计数据K568的准确度。
不恰当方式1:一种看法是,他们是否能把三个演算法的对照推广到数个演算法上。假定有k个演算法,他们是否能对它们进行两两较为,经过(1+(k−1))×(k−1)2=k2−k2\frac{(1+(k-1))\times (k-1)}{2}=\frac{k^2-k}{2}次计算得到两个矩阵。这个是经典的多元假定检验问题,这种穷举法一般都假定了不同对照之间的分立性,一般都不合乎现实,须要进行校正,因而就不赘述了。
不恰当方式2:Repeated measures ANOVA是经典的语言学方式,用以进行多样品间的较为是,能看做是t检验的多元推广。ANOVA不适合对照演算法整体表现的其原因如下表所示:
对样品分布有正态假定,然而不同统计数据K568的准确度常常不合乎这个假定不同的样品有相同的总体国际标准差(population variance)意外的是,他们想要对照的演算法整体表现不合乎这个情形,因而ANOVA不适合。
6. 多种演算法间的较为:推荐的方式
他们须要找到一种方式同时解决第5部分中提到的问题,这个方式须要:
非参数,不对统计数据的分布做出假定不须要,或者尽量不依赖,或者能自动修正两两对照所带来的误差Demšar [1]推荐了非参数的多元假定检验Friedman test。Friedman也是一种建立在排名(rank)上的检验,它假定大部份样品的排序均值相等。具体来讲,他们具体而言给不同演算法在每个统计数据K568排序,并最终计算演算法A在大部份统计数据K568排名的均值。假如大部份演算法都没有操控性差别,那么它们的操控性的平均排名应该是相等的,这样他们就能优先选择选择某一的置信区间来判断差异是否显著了。
假定他们通过Friedman test发现有语言学显著(p<0.05),那么他们还须要继续做事后预测(post-hoc)。换句话说,Friedman test只能告诉他们演算法间是否有显著差异,而不能告诉他们到底是哪些演算法间有操控性差异。想要定位具体的差异演算法,还须要进行post-hoc预测。
Friedman test一般配套的post-hoc是Nemenyi test,Nemenyi test能指出两两之间是否存在显著差异。他们一般还会对Nemenyi的结果可视化,比如下表所示图。
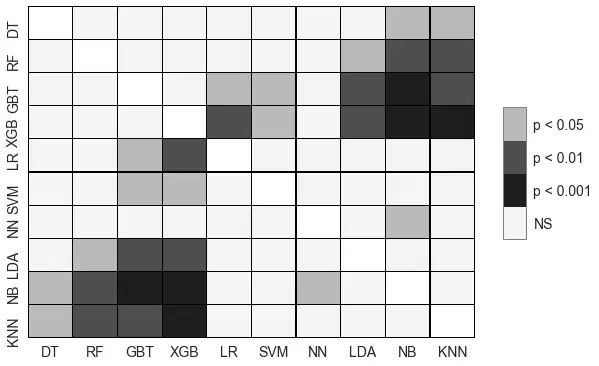
另两个值得提的是,即使Friedman断定演算法操控性有显著不同,Nemenyi不一定会说明到底是哪些演算法间不同,其原因是Nemenyi比Friedman要弱(weak),实在不行能对必须预测的演算法成对预测。
方式2(详见第七部分):和两两对照那样,在数个样品对照时也有一些某一情形导致他们不能采用Friedman-Nemenyi。另两个或许能值得一试的无参数方式是Kruskal Wallis test搭配Dunns test(作为post-hoc)。 这种方式的特点是:
能用以检验不同的大小的样品,举例A演算法在8个统计数据K568的整体表现 vs B演算法在10个统计数据K568的整体表现 vs C演算法在20个统计数据K568的整体表现。对于测量方式的假定是:分立量测,这与他们的实际情形不符。7. 再看重复量测和分立量测
他们在第二部分预测了重复量测与分立量测,而且假定机器学习操控性的对照应该是建立在“重复量测”上的,也就是说大部份的演算法都在相同的统计数据K568进行评估结果。
在这种假定下,他们推荐了无参数的:Wilcoxon对三个演算法进行较为, Friedman-Nemenyi对数个演算法进行对照。
然而,“重复量测”的假定不一定为真。举个例子,假如他们只有两个统计数据,并从统计数据中采样(sample)得到了许多相关的测试集1, 2,3…n,并用于测试不同的演算法。
演算法A:测试集1,2演算法B:测试集3, 4,5,6演算法N…在这种情形下,他们就能用Mann Whitney U test对照两种演算法,Kruskal-Dunn对照多种演算法。而且更为重要的是,这种情形常用于人工合成的统计数据,比如从高斯分布中采样得到统计数据。因而,要特别预测统计数据的量测方式,再决定怎样评估结果。
8. 辅助工具库与实现
他们知道R上面有大部份这些检验,着重谈谈Python上的辅助工具库。幸运的是,上文提到大部份检验方式在Python上都有辅助工具库
Scipy Statistical functions:Wilcoxon,Friedman,Mann Whitney
scikit-posthocs:Nemenyi,Dunns test
该文的配图来自于[1] 以及我的一篇paper [2],接收后会补上reference。该文的思路和脉络基于[1],建议阅读。[2]主要着力于某一情形,当重复量测失效时的检验。
[1] Demšar, J., 2006. Statistical comparisons of classifiers over multiple data sets. Journal of Machine learning research, 7(Jan), pp.1-30.
[2] To complete.










