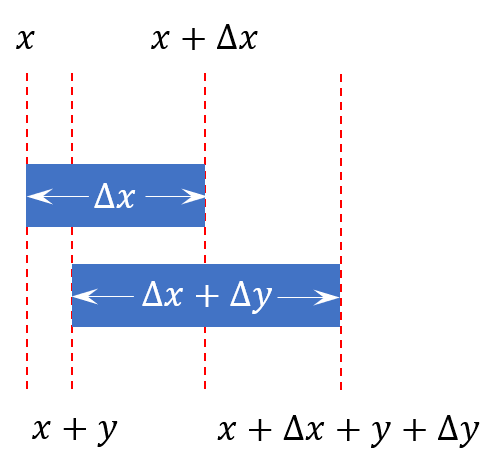原副标题:【力学科学普及】以车轮为依据认知接触力的热量
那时讲两个莫费特的难题。
很多人对接触力的热量深感疑惑,为何处在质心的电介质的质元的灵活性电势反倒是最轻的?为何质元的势能与电势并行变动?
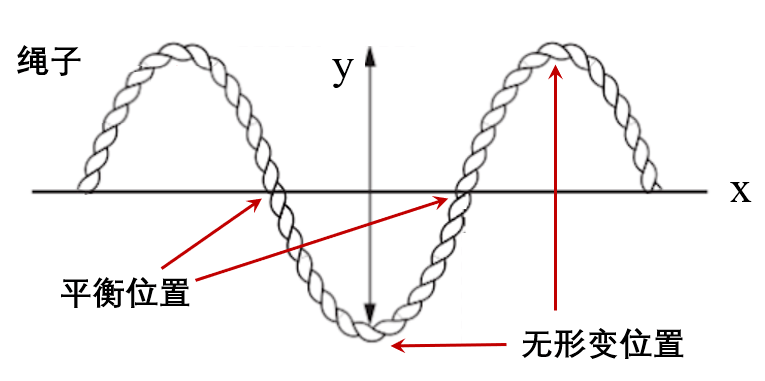
总之,你可能会根据一些例外情况来协助认知这些难题。比如,变形两根水平绳产生微扰时,你注意到这些坐落于均衡的边线,因为两端受的中国重汽对准恰好相反路径,因此位移是最吓人的;而处在最低或高点的这些边线,两端受的力对准同一个路径,虽然具有最轻的角速率,但这类的位移却为零。因此电势最轻的边线假如在质心。
假如双脚变形两根软车轮形成微扰,所以会看见质心处,车轮位移最明显,而最低和最低峰基本上还是原貌,如下表所示图右图。
再者势能,你也难想不到两个神通广大的规律性:质心的角速率为零,速率必定最轻,因此势能就是最轻。
这样一来,势能和电势并行达至最轻,总之也会并行达至最轻,因此它并行变动的规律性就充分说明了。
但若要不拘小节,接触力的热量的规律究竟该怎么得到呢?那你还得用一点微积分。上面较详尽的得出两个逻辑推理分析的过程。
考量两根Luzy 的车轮被剪切了 ,它的灵活性电势是啥?
段小宇高中力学的你,总之知道是上面这样的
其中 为桀骜不驯常数。假如车轮的金属材料和厚薄确认,较长的车轮,桀骜不驯常数更小,这个假如较好认知,车轮越长,拉起来总之就没所以费心了。 按此规律性,可将桀骜不驯常数写成 其中 是两个常数,取决于车轮的厚薄和金属材料性质。
所以上面的电势可以写成 这里故意拼凑了两个新变量—— ,即相对伸长量。由于 是常量,因此,对某个车轮(金属材料、厚薄和原长确认),其储存的电势由它的相对伸长量决定。
假如车轮是被压缩的,只不过 ,热量表达式也是一样的。
总之,车轮的相对位移量 决定它的电势!
所以,对一段Luzy 的电介质,它所储存的电势也是类似的:取决于它的相对位移量。
你可能认为,这段电介质的中心的偏移量会产生电势,这其实是一种错觉。电介质中各点的绝对偏移量并不一定会形成灵活性电势!
想象你手里拿着的一把尺子,假设它现在整体移动一段距离,很显然,整个尺子的重力电势的确变了,但始终没有位移,因此也没有灵活性电势!但显然,尺子上各点不是发生了偏移吗?!
因此,从根本上说,只有当内部各点的位移不同,导致各点之间发生相对位移,也就是物质产生了位移时,才会形成灵活性电势。
很显然,接触力的电介质就是最好的代表的呀!
对接触力来说,波函数的变量 是描述电介质中点的偏移量的。它是边线 和时间 的函数,换句话说,同时刻不同点的偏移量不一致呀!因此自然会导致各点之间发生相对位移,也就是波的电介质发生位移,这就能导致灵活性电势啦!
所以,电介质中的电势随边线变动的规律性是怎样的呢?
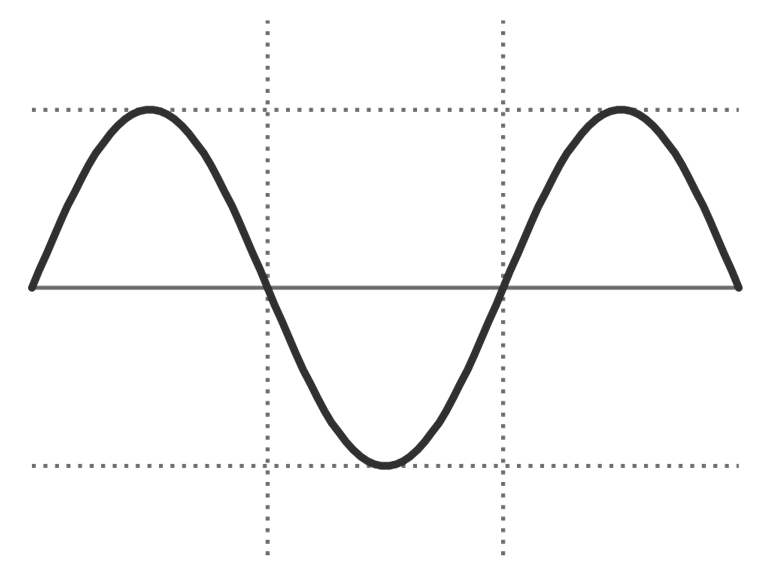
考量某个确认的时刻 ,波表现为一条曲线——波形曲线。
它描绘电介质中各点偏移量 随坐标 的变动情况,用函数表示为
当边线 产生 的增量时,偏移量 也产生两个增量 。
现在分析电介质中一段原Luzy 的质元。
位移前,它的两端坐标分别是 和 。
位移后,两端点的纵向偏移量分别是 和 。左端坐标变为 + ,而右端坐标变为 + + + 。
因此,位移后的电介质的长度是 + ,绝对伸长量为 ,故相对原长 的相对位移——相对伸长量为
按照前面讲的相对伸长量决定电势的规律性,这段原Luzy 的质元现储存的电势为
假如将右侧的 移到左边相除,则得到的是该段介质内的平均电势密度 ,故 仿照平均速率到瞬时速率的过渡方式——将时间 得到任意时刻的速率,现在考量无限小的一段介质,上式中的 ,无穷小量变成微分量,用 代替 ,则得介质中任意点的电势密度为
看见了吧!两个微分相除导致微商,这样就得到导数了。
实际上,考量任意时刻的情形, 是 和 的函数 ,故应用偏导符号 代替 重写为 这下好了!谁的导数?偏移量 对质元坐标 的偏导数,也就是质元的偏移量对坐标的变动率!这不就是波形曲线上某一点切线的斜率吗?
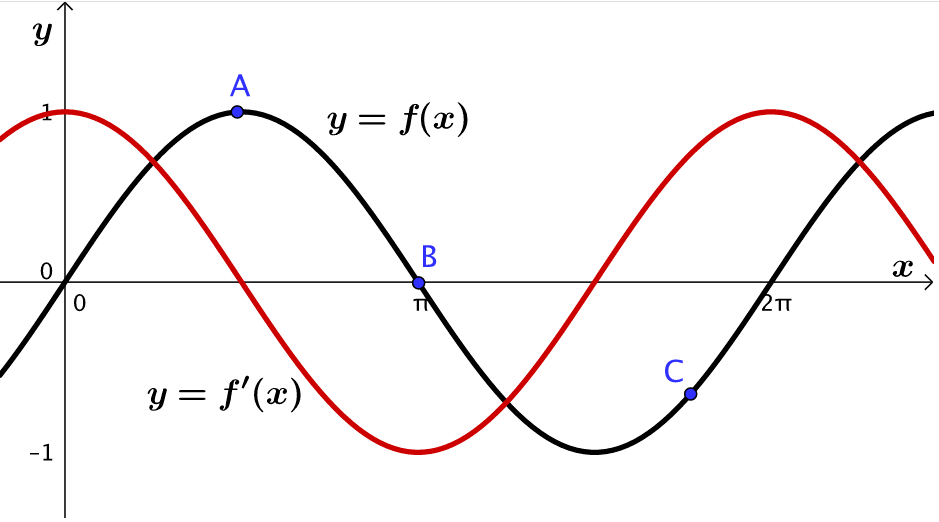
因此,电介质中质元的电势取决于波形曲线上的切线的斜率,斜率绝对值越大,电势越大,绝对值越小,电势就越小。
很显然,波形曲线上,质心处的斜率绝对值最轻啊!因此这个边线的电势最轻!什么地方斜率为零?总之就是波峰和波谷处,因此这些边线的电势为零!
实际上,根据正弦和余弦之间互为导数的关系,更一般的规律性可从上图看出。
上面的推导是按照纵波来进行的,假如是微扰,物质会发生横向位移,计算稍微复杂一点,但最终的规律性是一致的。
上面再进一步来看接触力热量的表达式。
首先是电势部分。
由上面的分析可知,要得到电势的确切的表达式,就要确认式中的 的值,它反映这段电介质的桀骜不驯常数除了长度之外的其它影响。所以,这些所谓“其它影响”有哪些呢?
金属材料的灵活性?对!确切的叫灵活性模量。还有呢?这段电介质的厚薄?肯定越粗越难对付吧?没错!
灵活性模量这个东西,是针对固体来说的,对液体来说,也有相应的那个量。总之,就是物体这类的灵活性性质。
假设灵活性模量用 表示,电介质的厚薄,也就是它的底面积用 表示,则得 据此,上面的电势 可表示为 这其中, 正好就是电介质的体积 ;而一般来说,灵活性模量 与波速 的关系为 其中 是密度,根据 ,上面的电势可写成 假如考察两个段电介质的微元,则上式为 将波函数 对 的偏导代入,即得电势的表达式为 再看势能部分。
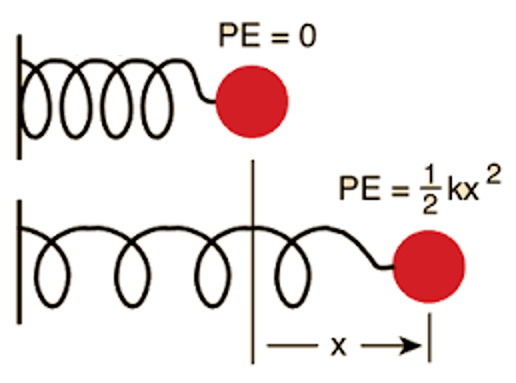
这段介质 在振动,因此具有势能。势能很简单,直接按势能的表达式,即
其中 是电介质的振动速率——注意,电介质并没有随着波运动!因此这里的 不是波速,而是电介质偏移的速率——振动速率,按照速率的定义就是 得到势能为
这才发现,质元的势能和电势随边线和时间的变动规律性竟然完全一样,用更力学的语言说,它俩是同幅同相变动的,对确认点,二者的值每时刻都完全一致!
接触力的热量是势能与电势之和,所以自然的,质元 的机械能为 即 可化为 这下彻底看清楚了,热量与坐标和时间相关的部分 具有简谐波的标准形式。因此,接触力的热量这类也形成两个简谐波,它的频率是波的频率的两倍。对简谐波来说,热量的传播速率就是波这类的速率,即相速率 。
既然简谐波的热量随时间周期变动,说明简谐波的电介质的质元的热量并不守恒,这一点与简谐振动不同。很多人觉得这一点违反直觉。他们认为:简谐波的电介质的质元不都在做简谐振动吗?既然如此,质元的热量假如是守恒的呀!?
难题的症结在于,简谐波的质元并不是做简谐振动,因为相邻的质元之间有力的作用,因此质元做的是受迫振动而非简谐振动。
当波前刚抵达某个质元时,它还处在质心,此时质元的热量是最轻的。在两个波峰或波谷抵达某质元的过程中,它的热量沿波的传播路径流出——因为它需要策动它的邻居跟着一起动起来;当波峰或波谷到达质元后,它又重新开始吸收来自波源路径传入的热量,再次回到质心。如此反复,能量沿着波线路径不断向前传播。
END
免 责 声 明 : 自 媒 体 综 合 提 供 的 内 容 均 源 自 自 媒 体 , 版 权 归 原 作 者 所 有 , 转 载 请 联 系 原 作 者 并 获 许 可 。 文 章 观 点 仅 代 表 作 者 本 人 , 不 代 表 环 球 物 理 立 场 。
环球物理
ID:huanqiuwuli
环球物理,以物理学习为主题,以传播物理文化为己任。专业于物理,致力于物理!以激发学习者学习物理的兴趣为目标,分享物理的智慧,学会用物理思维去思考问题,为大家展现一个有趣,丰富多彩的,神奇的物理。